Halme
by Kira Stöwe ed>Deutsch >Englisch
Kunst aus Halmen
>Einleitung >Benötigt >BeispieleEinleitung
>Basteln mit Stroh >Basteln mit Trinkhalmen >Vorgeschichte >Andere >WorkshopBasteln mit Stroh
In der Weihnachtszeit wird man oft besinnlich, backt oder gestaltet etwas für das Fest. Man kann z.B. Strohsterne oder Strohpuppen basteln. Dabei werden viele Strohhalme kunstvoll zusammen gebunden. (Die Bilder zeigen gekauften Schmuck.)


Basteln mit Trinkhalmen
Hier zeige ich nicht, wie man Strohalme bindet, sondern wie man Trinkhalme aus Plastik mit Nadel und Fäden verbindet. Dazu näht man dünne Fäden quer durch die Halme oder führt etwas dickere Fäden längs durch die Halme. Weiter kann es Fäden durch die Luft geben.
Stroh-, Plastik- und Papierhalme sind weitgehend austauschbar. Traditionell wird Stroh benutzt. Nach dem Verbot von Plastikhalmen werden vermutlich mehr Papierhalme aufkommen.
Ich nehme Plastikhalme wegen der gleichmäßigen Ware, wegen der dünnen Wände und wegen der Farbeigenschaften: Farben bei Licht und bei Schwarzlicht und Transparenz. Manche Halme haben Muster, z.B. Längsstreifen. Die können stören, besonders wenn man die Fäden in den Halmen sehen will.
Vorgeschichte
Ich habe mir das alles selbst ausgedacht. Doch wie kam ich dazu?Seit Jahren beschäftige ich mit geometrischen Objekten. Sie haben Ecken, Kanten und Flächen. Ich wollte sie mit meinen Händen realisieren und "begreifbar" machen. Das geht gut mit Papier: falten, schneiden, kleben. Wenn aber innere Flächen (Wände) das Objekt in Räume (Zellen) teilen, benutzt man Drahtmodelle für die Kanten und denkt sich die Flächen dazu.
Drähte kann man schneiden, biegen und löten oder schweißen. Sie sagten mir aber nicht besonders zu. Statt dessen versuchte ich es mit (ungekochten) Spagettis und Heißkleber. Das funktionierte, aber die Modelle waren zerbrechlich und wenig attraktiv. Dann kam ich auf die Idee mit den Halmen. Die finde ich attraktiv, und durch Farbwahl kann ich Teilstrukturen hervorheben. Aber sie schränken mich bei den Objekten stark ein - schon ein Quadrat lässt sich kaum herstellen.
So änderte ich mein Ziel: Ich baue mit Trinkhalmen schöne Objekte. Die neuen geometrischen Objekte berechne und visualisiere ich mit dem Computer und drucke ich groß auf Acrylglas aus. Beides stelle ich in besonderen Häusern aus.
Was machen andere Leute aus Halmen?
Zitat aus Wikipedia: "Himmeli ist eine aufwendige Bastelei aus Stroh, die in Finnland, Litauen, Lettland und Schweden eine beliebte Weihnachtsdekoration darstellt."Ich suchte z.B. ein wenig nach Halm, basteln, straws, tinker und himmeli und fand dabei Verschiedenes. Beispiele:
- Fäden längs und quer durch Plastikhalme wie hier, aber auch durch Papierhalme und durch echte Strohhalme
- Umgekehrt Benutzung von Plastikhalmen für "Strohfiguren" und für ganz andere Gebilde
- Häufig Oktaeder und ähnliche Objekte: einem waagerechten Ring aus Halmen mit Verbindungen zu zwei Punkten darüber und darunter
- Kombinationen von vielen solchen Objekten zu einem großen Himmeli
- Verwendung von Halm-Objekten als Schmuck an Gegenständen, als Pflanzenhalter und als Lampenschirm
- Ich achte bei Halmen und Fäden auf Farbe, Transparenz und Fluoreszenz.
- Ich achte auf genaue Fadenführung und auf das geordnete Zusammentreffen der Halme an den Ecken.
- Ich mache zusätzlich auch Verbindungen mit Fäden ohne Halme.
- Ich persönlich stelle besonders mathematische Objekte dar und freue mich über andere Werke.
Verbinder statt Fäden
Die hier gezeigte Technik finde ich besonders interessant. Dabei werden keine Fäden benutzt, sondern Verbinder mit Ärmchen, die in die Halme geschoben werden. Die Verbinder werden mit einem Lasercutter aus einer Plastikscheibe geschnitten. Es gibt Verbinder mit 3,4,5 und 6 regelmäßig angeordneten Ärmchen.Vorteile: Einfache, genaue und stabile Montage
Nachteile: Die Halme zweigen alle in einer Ebene ab. Nur bestimmte Objekte können damit gebaut werden.
Ich hatte auch schon an Verbinder gedacht, ohne diese Nachteile: An den Ecken sind Kugeln und in den Halmenden stecken Verbinder zur Kugel. Dazu gibt es zwei Versionen:
- Der Verbinder hat eine Spitze, die in die Kugel gedrückt wird.
- Der Verbinder hat zwei Magnetpole, die an der Kugel andocken (von mir bevorzugt, falls machbar).
Workshop
Es gab einen Workshop zum Gestalten mit Trinkhalmen.| Zeit | Donnerstag, 29.11.2018, 15-18 Uhr |
|---|---|
| Ort | Goldammerweg 28, 50829 Köln-Vogelsang, Eingang an der Rückseite des hohen Hauses |
| Kontakt, Anmeldung | Leiterin Petra Gräff: 0221/9920 3977, petra.graeff@koelner-senioren.de |
| Vortragende | Kira Stöwe, 0221/550 1024, kira-s@gmx.de |
| Mitbringen | Man muss nicht unbedingt etwas mitbringen.
Empfehlung: eine Brille, eine Schere und eine Tasche zum Transport
Ihrer Kunstwerke.
Halme und Fäden für eine erste Übung sind vorhanden.
Man kann aber auch gerne mehr mitbringen, s. "Benötigt". |
| Teilnehmer | Neben den Senioren, die sich hier treffen, sind auch andere Teilnehmer gern gesehen. Z.B. Künstler, Bastler, Raumgestalter, Presse und besonders Kinderbetreuer. |
| Aussichten | Auf Wunsch wird der Workshop woanders wiederholt. Auch eine Bastelgruppe kann entstehen und unterstützt werden. Kunstwerke, Techniken und Ideen können veröffentlicht und mit anderen ausgetauscht werden. |
Benötigt

Ausrüstung
>Ein Behälter>Halme
>dünnes Garn, dazu Nähnadel und Einfädler
>ein etwas dickeres Garn, dazu längere Nadel und Magnet
>oder statt großer Nadel und Magnet eine "Holznadel"
>Schere
>Eventuell Längenmaß, Perlen und Schwarzlicht
Fähigkeiten
>Genügend Sicht, etwas Fingerfertigkeit, Ideen, FantasieBenötigt: ein Behälter
Auf dem Bild ist der Behälter eine Eierschachtel. Benötigt wird er zum Zusammenhalten der Hilfsmittel. Reste von Halmen und von Fäden brauchen vielleicht auch einen Behälter.Benötigt: Halme
Die Halme aus Plastik und die Garne können schwarz, weiß, farbig, und transparent sein und bei Schwarzlicht fluoreszieren.Die Halme halten nicht ewig. Besonders fluoreszierende Halme zerbröseln bald bei Sonnenlicht.
Plastiktrinkhalme soll es ab etwa 2021 in der EU nicht mehr geben, ähnlich wie jetzt schon Glühbirnen. Das soll den Müll in den Meeren mindern. Anscheinend gelangen bisher Unmengen von Halmen aus Deutschland ins Meer.
Benötigt: dünnes Garn, dazu Nähnadel und Einfädler
Dieses Garn soll mit der Nähnadel quer durch Halme gestochen und geführt werden.Es gibt auch Nähnadeln mit einem Einfädelschlitz am Öhr, damit entfällt der Einfädler.
Benötigt: ein etwas dickeres Garn, dazu längere Nadel und Magnet
Dieses Garn soll mit der Nadel längs durch mehrere Halme geführt werden.Oft werden mehrere Fäden durch denselben Halm geführt. Deshalb darf das Garn nicht zu dick sein und die Nadel nicht spitz sein.
Der Magnet dient dazu, die Nadel durch den Halm zu ziehen.
>Einfädeln >Faden durch Halm ziehen
Einfädeln




Normalerweise braucht man viele Fäden für ein Objekt. Das übliche Einfädeln von Hand oder mit Einfädler ist mühsam. Eine wenig attraktive Alternative ist, einen ziemlich langen Faden zu nehmen, jeweils weit durchzuziehen und das hintere bearbeitete Stück abzuschneiden. Ich benutze folgende Alternative für das dickere Garn:
- Vorbereitung: Ein Stück dünnen Faden durch das Öhr der abgerundeten Nadel führen und die Enden verknoten.
- Mit Daumen und Zeigefinger die Öse so aufnehmen, dass beide Finger jeweils in einer kleineren Öse sind.
- Diese aufeinanderlegen und ca 1 cm vom dickeren Faden hindurchführen.
- Die kleinen Ösen zusammenziehen.
- Die Befestigung reicht aus, um die Nadel durch Halme zu ziehen. Danach lässt sich der dünne Faden leicht abstreifen und wieder verwenden..
Faden durch Halm ziehen

- Dickeres Garn in die lange Nadel fädeln.
- Vorderes Nadelende in den Halm stecken.
- Mit dem Magnet die Nadel durch den Halm ziehen.
Holznadel



>Was ist eine Holznadel? >Herstellung >Verwendung >Hindernisse
Was ist eine Holznadel?
Der Begriff ist von mir. Ich nehme einen hölzernen Schaschlikspieß oder für längere Halme einen hölzernen Pflanzenstützstab. Die Form ist ein länglicher Zylinder mit einer Spitze davor. Er muss dünn genug sein, so dass er durch die Halme passt zusätzlich zu den schon durchgezogenen Fäden. Am Ende des Zylinders wird eine Kerbe gemacht, durch die man den Faden in einen Schlitz einbringt.Herstellung der Holznadel
- Mit einem scharfen Messer schneide ich vom Ende aus 2 bis 4 cm tief in den Stab.
- Ich ziehe das Messer etwas zurück, stecke einen Offenhalter, z.B. eine Nadel, in den Spalt und entferne das Messer.
- Mit einer Feile schräge ich die Endstücke ab, so dass nach Wegnahme des Offenhalters ein Keil im Ende ist.
- Ich markiere den Keil farblich, so dass die Richtung gut zu sehen ist und entferne den Offenhalter.
- Damit ist die Holznadel fertig. Bei Serienherstellung reicht am Ende etwa eine Minute je Nadel.
Verwendung der Holznadel
Die Nadel wird dazu benutzt, Fäden längs durch Halme zu ziehen. Der Anfang des Fadens wird quer über den Keil gelegt und nach vorne in den Spalt gezogen. Er soll bei der Nutzung halten, aber den Spalt nicht verlängern. Mit der Nadel wird der Faden durch die Halme gezogen. Am Ende wird der Faden verknotet, von der Nadel genommen und geschnitten.Hindernisse bei der Bewegung der Holznadel
Manchmal versperren schon angebrachte Halme oder Fäden die Bewegung der Nadel. Dann muss man den Faden vorübergehend von der Nadel nehmen.Benötigt: Schere
Die Schere dient zum Schneiden von Halmen und Fäden. Die Größe ist unwichtig.Achtung: Wenn der Magnet die Schere berührt, wird sie sofort dauerhaft magnetisch und zieht unter anderem Nadeln an.
>Halme schneiden
Halme schneiden

- Ersten Halm schneiden und senkrecht auf eine glatte Fläche stellen.
- Weitere Halme einzeln rechts daneben stellen.
- Eine geöffnete Schere auf den linken Halm legen und von rechts zuschneiden.
Benötigt: Eventuell Längenmaß, Perlen und Schwarzlicht
Längenmaß
Zweck: Bestimmen von Halmlänge und Größe eines Objekts und seiner Teile.Perlen
Zweck: Verzierungen, waagerechte und senkrechte Stabilisierung, leiches An- und Abhängen von Teilen. (Das trifft alles bei meinem Mobile zu.)Schwarzlicht
Das ist unsichtbares UV-Licht, das manche Farben zum Leuchten bringt.Zweck beim Basteln: das spätere Aussehen testen.
ACHTUNG: Schwarzlichtröhren enthalten wie andere Leuchtröhren und Energiesparlampen Quecksilber. Während des Betriebs ist dieses gasförmig. Bei einem Bruch verteilt es sich im ganzen Raum, vergiftet die Anwesenden und setzt sich überall fest.
Scharzlichtlampen werden leicht übersehen. Im Dunkeln kann man leicht daran stoßen oder über Schnüre stolpern.
Fähigkeiten: Genügend Sicht, etwas Fingerfertigkeit, Ideen, Fantasie
Diese Fähigkeiten haben und trainieren besonders Kinder. Aber für Senioren ist es um so wichtiger, die Fähigkeiten zu trainieren.Beispiele
>Dreieck >Tetraeder >Fünfzell >Oktaeder >Nachbearbeitung >Kreuze{3} Dreieck






Konstruktion mit Nadel und Magnet
- Faden mit der Nadel und Magnet längs durch 3 Halme führen. Magnet weglegen.
- Die Enden der Halme zusammen legen. Faden aus der Öse befreien.
- Die Fadenenden dreifach verknoten und abschneiden.
Konstruktion mit Holznadel
- Faden mit der Holznadel längs durch 3 Halme führen.
- Die Enden der Halme zusammen legen.
- Die Fadenenden dreifach verknoten und abschneiden.
Geometrie
Wenn die Halme gleich lang sind, erhält man ein gleichseitiges Dreieck, auch regelmäßiges oder reguläres Dreieck genannt. Im folgenden benutzen wir oft solche Dreiecke und andere reguläre Formen.Nach einer vom Mathematiker Schläfli eingeführten Notation hat es das Schläfli-Symbol {3}. (Nicht zu verwechseln mit dem erst später eingeführten Symbol {3} für eine Menge)
{3,3} Tetraeder (oder regelmäßige dreiseitige Pyramide)




- Ein Dreieck bauen und durch eine Seite (gelb) einen Faden ziehen.
- Den Faden auch durch zwei weitere Halme (rot und blau) führen und die Enden verknoten. Das Bild zeigt einen Rhombus mit einer Diagonale.
- Einen Faden durch zwei seiner Kanten (rot, blau) führen und durch einen weiteren Halm (gelb).
- Die Enden zusammen bringen und verknoten.
- Auch die letzten drei Halme, durch die nur ein Faden führt, als Dreieck verbinden.
- Der Tetraeder ist fertig. Jedes Dreieck hat Kanten in 3 Farben mit einem gemeinsamen Faden.
Geometrie
Das Schläfli-Symbol {3,3} bedeutet: Dreiecke, je 3 an jeder Ecke.{3,3,3} Fünfzell

>Konstruktion >Geometrie
Konstruktion
- Einen Tetraeder bauen wie zuvor beschrieben.
- Ein nicht ganz dünnes, etwas elastisches Garn wählen.
- 2 Fäden davon abscneiden, jeweils etwa dopplt so lang wie ein Halm.
- Ein Ende von innen durch die Fäden einer Ecke nach außen ziehen und (<--todo-->wie bei Nacharbeiten noch beschrieben werden soll) anbringen.
- Das andere Fadenende beim anderen Ende des blauen Halms durchziehen, aber noch nicht befestigen.
- Mit dem zweiten Faden dasselbe beim zweiten blauen Halm tun. Dabei sollen sich beide Fäden in der Mitte umschlingen.
- Von außen an den Fadenenden ziehen bis alles stramm und symmetrisch ist.
- Einen Faden anbringen, dann den zweiten wieder stramm ziehen und auch anbringen.
Geometrie
Warum der Name Fünfzell?
Die 6 Halme und die vier inneren Fadenhälften werden alle als Kanten gesehen. Es gibt außer dem äußeren Tetraeder noch vier innere Tetraeder. (Sie sind abgeflacht. Sie haben jeweils ein äußeres Dreieck mit 3 Halmen und drei Fäden zum Mittelpunkt. Damit werden drei weitere Flächen gebildet.) Die so umschlossenen Räume werden Zellen genannt, ebenso der Außenraum, insgesamt 5 Zellen.Das geometrische Objekt und sein Bild


Ebenso ist unser Fünfzell ein Bild von einem 4-dimensionalen regelmäßigen Fünfzell.
Das ist zunächst nur eine Analogie. Wir leben im Raum mit 3 Dimensionen, können eine 4. Raumdimension nicht erleben, aber ein Bild von einem 4D-Objekt machen.
Der 4-dimensionale Raum
Aber was ist denn die 4. Dimension. Sicher nicht die Zeit, sie ist anders,
geht von der Vergangenheit zur Zukunft. Die 4. Dimension hat nichts mit
unserer Erfahrung zu tun, sondern ist ein mathematisches Konstrukt:
- Wenn wir eine Gerade mit zwei Punkten 0 und 1 haben,
können wir für jeden Geradenpunkt mit einer Zahl x angeben, wo er ist.
- In der Ebene benutzen wir ein Koordinatensystem. Für jeden Punkt P
können wir mit einem Zahlenpaar (x,y) oder (p1,p2) den Ort
angeben. Wir identifizieren den Punkt auch mit seinem Ort: P=(p1,p2).
- Im 3D-Raum ist ein Punkt durch 3 Zahlen gegeben: (x,y,z) oder
P=(p1,p2,p3).
- Dann gehts einfach weiter: Der vierdimensionale Raum besteht aus allen
Punkten P=(p1,p2,p3,p4).
Bei jeder weiteren Dimension kommt eine Zahl hinzu.
Die ganze Geometrie der Ebene und des 3D-Raumes kann man durch Zahlen
ausdrücken und auf mehrdimensionale Räume erweitern. Die Anschaulichkeit geht
dabei allerdings verloren.
Schläfli-Symbole
Der Fünfzell hat das Schläfli-Symbol {3,3,3}, weil jede Kante
3 Tetraedern {3,3} um sich hat. Bitte nachprüfen!
Zu allen 5 platonischen Körpern gibt es vierdimensionale Entsprechungen:
| {3,3} Tetraeder | {3,3,3} 5-Cell |
| {3,4} Oktaeder | {3,3,4} 16-Cell |
| {4,3} Hexaeder | {4,3,3} 8-Cell |
| {3,5} Icosaeder | {3,3,5} 600-Cell |
| {5,3} Dodekaeder | {5,3,3} 120-Cell |
| keine Entsprechung | {3,4,3} 24-Cell |
Das Schläfli-Symbol {s1,s2} oder {s1,s2,s3} bedeutet die Zahl der Kanten einer Fläche, die Zahl der Flächen einer Zelle und die Zahl der Zellen um eine Kante. Die 4d-Obbjekte kann man in 3D abbilden (s. o.{3,3,3}). Alle Halmobjekte mit 3 am Anfang sind stabil. Allerdings ist {3,3,5} ziemlich groß.
{3,4} Oktaeder
>Konstruktion >Geometrie >SpitzenKonstruktion eines Oktaeders
Gute stabile Konstruktion


- Wie beim Tetraeder zuerst ein Dreieck machen (linkes Bild, unten grün)
- An jede Kante mit zwei schwarzen Halmen ein Dreieck anfügen
- Aus zwei der schwarzen Kanten und einem grünen Halm jeweils ein Dreieck einfügen
- Im oberen grünen Dreieck einen Faden spannen
Alternative Formulierung der Konstruktion
- Ein erstes Dreieck machen
- Weitere gleichseitige Dreiecke anfügen
- Dabei beachten, dass an jeder Ecke genau 4 Halme zusammen kommen.
- 3 ⇒ {3,3} Tetraeder
- 4 ⇒ {3,4} Oktaeder
- 5 ⇒ {3,5} Ikosaeder
- 6 ⇒ {3,6} Füllung der Ebene mit Dreiecken
Dabei muss man irgendwann aufhören. - 7 ⇒ {3,7} und mehr: Füllung der der hyperbolischen Ebene mit Dreiecken. Das lässt sich mit Halmen kaum machen.
Schlechte Konstruktion
VorgesehenGeometrie von Oktaeder und Hexaeder (Würfel)
Der Oktaeder {3,4}
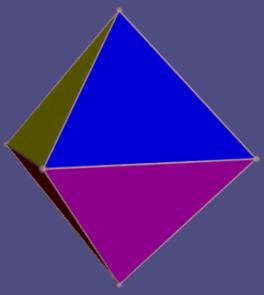
- Er hat 8 Dreiecke, von denen je 4 an einer Ecke zusammen kommen, 12 Kanten und 6 Ecken.
- Er ist regulär (regelmäßig) d.h. zu je 2 Kombinationen zusammen gehöriger Ecke, Kante und Fläche gibt es eine Raumsymmetrie, die das Objekt auf sich selbst abbildet die Kombinationen aufeinander.
- Er ist ist eine vierseitige Doppelpyramide. Sie besteht aus einer vierseitigen Pyramide nach oben und einer nach unten.
- Bei vielen altägytischen Pyramiden empfindet man intuitiv den unteren Teil mit und verdoppelt dadurch ihre Größe. >Pyramiden
Die intuitive Ergänzung der Pyramiden zu Oktaedern liegt an ihrem
damals bewusst gesetzten Neigungswinkel von etwa 54°44'. Das ist der
Winkel des Oktaeders mit gleichseitigen Dreiecken. Beispiele sind
die 3 großen Pyramiden bei Gizeh.
- Cheops-Pyramide: Regierungszeit 2620 bis 2580 v. Chr., 146,6 m hoch, Neigungswinkel 51°50'40"
- Chephren-Pyramide: Regierungszeit 2558 bis 2532 v. Chr., 143,5 m hoch, Neigungswinkel 53°00'10"
- Mykerinos-Pyramide: Regierungszeit 2532 bis 2503 v. Chr., 65 m hoch, Neigungswinkel 51°50'
Der Hexaeder (Würfel) {4,3}

- Er hat 6 Vierecke, von denen je 3 an einer Ecke zusammen kommen, 12 Kanten und 8 Ecken.
- Er ist regulär (regelmäßig)
Zusammenspiel
Mit Spitzen


Auf jedes Dreieck des blauen Oktaeders ist eine rote Spitze aufgesetzt.
Die Spitzen bekommen goldene Kugeln. Die acht Kugeln sind die Ecken eines Würfels. Wenn man benachbarte Kugeln verbindet, bekommt man seine Kanten.
Die Kugeln sind gekaufter Weihnachtsschmuck aus Styropor mit Goldglitzer. Ein dünner, bei Schwarzlicht leuchtender Faden ist hindurch und zurück genäht, geknotet und stramm mit der gegenüber liegenden Kugel verbunden. Diese vier Diagonalfäden treffen sich in der Mitte.
Nachbearbeitung
VorgesehenKreuze

Ein Kreuz mit quadraticher Verspannung.
Dieser Verlauf mit einem einzigen Faden wird auch bei weiteren Kreuzen benutzt

Drei zueinander senkrechte Kreuze wie das vorige.
Die Ecken und die äußeren Kanten bilden einen Oktaeder.
Weil die 3 Halme nicht alle an derselben Stelle im Mittelpunkt sein können sind sie zueinander versetzt. Das fällt bei diesen kurzen Halmen besonders auf und wäre bei langen Halmen nicht so schlimm.
Bei diesem 3D-Kreuz sind die drei Halme durch 3 Paare paralleler Halme ersetzt. Jedes Paar verläuft in der Mitte durch ein anderes Paar und wird von dem dritten Paar umschlossen.
Durchsichtige durchlochte Halmstücke sorgen für den Abstand der Halme eines Paars.

Ein blaues Kreuz als christliches Symbol.
Die beiden Halme sind durch ein kurzes Fädchen vernäht, damit sie nicht verrutschen. Man kann eine Schlaufe als Aufhänger hinzutun.

Ein Kreuz aus langen vernähten Halmen
English
There is no English translation. May you do it?Then please contact me at kira-s@gmx.de.
