← 0 →
red and gree on blue

Kira Stöwe

ed Geometrische Kunst und mehr / Geometric art and more
© Alle Rechte vorbehalten / All rights reserved
 >Deutsch  >Englisch

Willkommen auf meinen Seiten.

Ihr könnt sie gerne bekannt machen, Links darauf setzen und mir das melden. Aber kopiert bitte nichts von mir ohne mich zu fragen.
 >Ich, Kontakt  >ausgewählte Bilder  >Kunst  >Mathematik  >Links

Ich, Kontakt

Telefon / Phone Kira

Kontakt

Ich, Frau Kira Stöwe, bin erreichbar bei
kira-s@gmx.de, +49-221-5501024

Verlinken und kopieren

Ihr könnt meine Seite kira-s.de gerne bekannt machen, Links darauf setzen und mir das mitteilen. Aber kopiert bitte nichts von mir ohne mich zu fragen.

Bilder in diesem Artikel

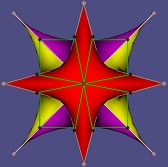
Hier gibt es viele Bilder, die euch hoffentlich gefallen. Die meisten sind von mir. Sonst gebe ich an, woher sie sind. Viele meiner Bilder sind geometrisch. Ich habe sie mit eigener Software berechnet und nichts weiter verändert. Manche zeige ich groß ausgedruckt bei Ausstellungen. Die Berechnungen dauern lange. Ich wiederhole sie mit Variationen bis mir ein Bild gefällt. Lehrer Lämpel

Mathematik

Ich verstehe, wenn viele Leute Mathematik nicht mögen. Negative Erwartung in der Gesellschaft und Unterricht auf ausgetretenen Pfaden machen es den Schülern schwer. Ich wünsche ein Angebot unterschiedlicher Zugänge zur Mathematik: rational, emotional, ästhetisch, systematisch, experimentell, spielerisch, spannend, anwendungsorientiert, geführt und frei.

Ich bin zwar didaktisch nicht gut, möchte aber meine Liebe zur Mathematik weitergeben. Mathematik ist schön! Das versuche ich mit meinen Bildern zu zeigen. Ich versuche es auch, indem ich meine Begeisterung und meinen Weg beschreibe. Außerdem will ich die Ergebnisse meiner Forschung darstellen. Aber das dauert noch etwas.

Erkenntnissse gewinnen

Ich will wissen, warum etwas so ist, wie es ist und wie etwas funktioniert Am liebsten kriege ich das selbst heraus, ignoriere deshalb oft, was andere Personen dazu gesagt haben. Beim Suchen und Forschen ist der Weg das Ziel. Dabei interessieren mich speziell allgemeine, zeitlose, schon lange gestellte Fragen.

Links

Ich mache Links...
  • zu eigenen Seiten und Bildern
  • zu externen Seiten mit inhaltlichem Bezug
  • als Linkaustausch, bisher nur:
    http://www.vivit944.de/, Glauben und Gemeinde: kopierte Bilder und Links zu kira-s.de
Haftung: Obwohl ich bei externen Seiten zunächst prüfe, dass keine auffälligen sittliche oder rechtliche Verstöße vorliegen, kann ich keine Verantwortung für den Inhalt übernehmen.
Einige Links führen zur Zeit in die Irre.
Alpen / The Alps by Dr. Elisabeth Stöwe
Alpen in Mutters Kunst
The Alps in mother's art
(Aquarelle 1992)
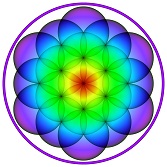
Lebensblume / Flower of life
Blume des Lebens in Galerie
Flower of life in Galery
(19 spheres and a torus)
Ein Oktaeder in Ausstellung 1
An octahedron in Exhibition 1
(Inside are black light objects)
7 Bilder in Ausstellung 2
7 Images in Exhibition 2
(50x50cm, based on polytopes)
Kaleidoskop in Ausstellung 3
Kaleidoscope in Exhibition 3
(in front of a polytope image)
Markuskirche in Ausstellung 4
Markus church in Exhibition 4
(Right wall: Images)
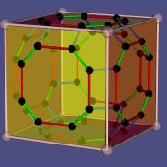
Würfel, Flaggraph Polytope 2004
Cube, flag graph Polytopes 2004
(Create your own polytope!)
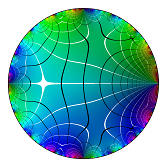
Verteilung von Primzahlen
Distribution of prime numbers
(∑p≤x, p prime1/p, x<4.3e9)
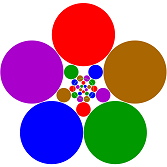
Komplexe Funktion in Abba
Complex function in Abba
u(x)=∏i=0,1,2,.. (1-x2i)
Abba and fair arrangements
Blume in Polytope 2013
Flower in Polytopes 2013
(Two polytopes in one image)

Kunst

Man kann verschiedener Meinung sein, was Kunst ist. Ich dachte, was ich mache, ist keine Kunst. Doch dann sagten andere, es sei eine ganz besondere Kunst. Ich gebe nach.
 >Galerie  >Ausstellungen  >Technik  >Bilder meiner Mutter  >Texte

Galerie

Galerie

Ausstellungen

 >Ausstellung 1: Oktober 2009 im Fort Paul, Köln
 >Ausstellung 2: Januar 2012 im Albert-Schweitzer-Haus, Bonn
 >Ausstellung 3: September/Oktober 2012 in der Gallery Plattforms, Köln
 >Ausstellung 4: September/Oktober 2013 in der Markuskirche, Köln
 >Ausstellung 5: Januar 2014 im Restaurant zur Sonnenblume, Köln

Ausstellung 1: Oktober 2009 im Fort Paul, Köln

Meine erste Ausstellung begann am 1. Oktober 2012. Sie zeigte 9 selbst gebastelte reale geometrische Objekte und 21 DIN A4-Blätter mit Laserdrucken: ein Blatt mit Einladungstext, 20 mit digitalen Bildern.
Zum Dokument

Ausstellung 2: Januar 2012 im Albert-Schweitzer-Haus, Bonn

Meine zweite Ausstellung begann am 8. Januer 2012. Sie zeigte digitale Bilder mit weiter entwickelter Technik und in besserer Qualität als zuvor. 15 der Bilder waren in hoher Auflösung und großem Format auf Alu Dibond hinter Acrylglas.
Zum Dokument

Ausstellung 3: September/Oktober 2012 in der Gallery Plattforms, Köln

Meine dritte Ausstellung begann am 29. September 2012. Zu sehen waren Bilder der vorigen Ausstellung, ein paar neue und handgemachte Objekte.
Zum Dokument

Ausstellung 4: September/Oktober 2013 in der Markuskirche, Köln

Meine vierte Ausstellung begann am 15. September 2013. Es waren 20 große Bilder zu sehen, davon 4 neue. In der schönen Markuskirche kamen sie besonders gut zur Geltung.
Zum Dokument

Ausstellung 5: Januar 2014 im Restaurant zur Sonnenblume, Köln

Meine fünfte Ausstellung war am 11. Januar 2014 vor ausgewählten Gästen.
Zum Dokument

Technik

Meine Kunst besteht aus vielen Bildern und ein paar Objekten. Einige davon wurden auf Ausstellungen gezeigt.
 >Technik für Bilder  >Technik für reale Objekte

Technik für Bilder

Die meisten Bilder sind auf Computern mit selbst geschriebenen Programmen berechnet und in Grafikdateien gespeichert (svg, png, jpg, bis zu 14000 Pixel in eine Richtung). Zur ersten Ausstellung wurden sie einfach mit einem Laserdrucker auf DIN A4-Papier gebracht. Seit der zweiten Ausstellung werden Fotopapier und Alu Dibond mit Acrylglas verwendet (bis zu 1m×1m).

Der Inhalt der Bilder basiert meist auf regelmäßigen mathematischen Objekten, die ich teilweise selbst entdeckt habe. Sie werden von meinen Programmen berechnet und entweder in die Ebene oder in den dreidimensionalen Raum projiziert.

Bei ebener Projektion werden sie als svg-Datei (SVG: Scalable Vector Graphik) gespeichert. Bei räumlicher Projektion werden sie in einer wrl-Datei (VRML: Virtual Reality Modelling Language) oder in einer pov-Datei (POV-Ray: Persistence Of Vision Ray tracing) gespeichert.

Die wrl-Datei wird mit einem VRML-Viewer angesehen. (Ich benutze Cortona3D, wüsste gern bessere Software.) Man kann dabei das Objekt und sich als Beobachter bewegen. Ich speicherte Screenshots davon, die Größe ist durch den Monitor beschränkt. Inzwischen nehme ich für das Endergebnis pov-Dateien. Sie können mit dem freien Programm POV-Ray in guter Qualität angezeigt und als Bilddatei gespeichert werden.

Technik für reale Objekte

Diese Objekte bastel ich. Meist benutze ich Trinkhalme. Mit einer Nadel führe ich Fäden dadurch, ein kleiner Magnet hilft dabei. Die Fäden verbinden mehrere Halme zu einem Objekt. Manchmal steche ich auch durch die Wand der Halme. Das ist in der Galerie bei dem Vogel und bei den zwei Bildern davor zu sehen.

Eine Anleitung ist hier: Bauen mit Halmen.

Bei der Ausstellung 1 hing in der Raummitte ein großer Oktaeder aus Latten und Dachpappe. Er ist auf der Ausstellungsseite beschrieben und zu sehen.

Bilder meiner Mutter

Dokument dazu

Texte

 >Vorwort  >Elfchen  >Monats-Elfchen 1  >Monats-Elfchen 2  >Ich bin

Vorwort

Ich schreibe keine anspruchsvollen Texte, sondern nur einfache Gedichte aus 11 Wörtern in Form eines Tannenbaums, Elfchen genannt. Zur Erläuterung davon gibt es die Seite "Elfchen" mit zwei Elfchen über Elfchen und mit vier Bildern von Elfen.

Es folgen zwei Seiten mit "Monatselfchen", mit Elfchen und Bildern zu jeden Monat im Jahr. Frau Gisela Kibele brachte mich auf die Idee dazu und lieferte die Inhalte der ersten Seite mit Monatselfchen.

Meine Bilder auf der ersten und der dritten Seite stammen von Wikimedia, die Links darauf und auf die Rechte sind angegeben. Alle Bilder sind zum Anklicken.

Weitere Elfchen von mir sind auf der Einladung zur 5. Ausstellung.

Ich bin

Das Gedicht ist eine Ausnahme, es hat mehr als elf Wörter. Der Anlass war: Ich ging mit einer jungen Frau im Park spazieren. Sie sah jemand, den sie kannte und stellte uns mit Namen vor. Er fragte mich: "Was bist du?" Ich hatte keine Lust auf eine Erklärung und sagte: "Ich bin ich, mehr brauchst du nicht." Normalerweise bin ich nicht so abweisend und sage auch etwas über mich.

Am nächsten Tag dachte ich darüber nach. Mir kam in den Sinn, meine Aussage klarer zu machen. Wieso sagt "Ich bin ich." schon viel über mich aus? Daraus entwickelte sich schnell das Gedicht, und ich schrieb es auf. Das hat mich überrascht.

Elfchen - Minigedichte wie Tannen

Elfen
wunderschöne Lichtgestalten
klein und fein
mystisch feenhaft kaum sichtbar

Elfchen

==
== ==
== == ==
== == == ==

==

Elfchen
elf Wörter
in fünf Zeilen
eins zwei drei vier

Schlusswort


Quellen, Autoren und Rechte der Bilder: Elfo_red, Elfe-Harmo-03, Skulptur einer Elfe, The-Nameless-Elf
Für meine (Kira Stöwe) Variationen der Bilder gelten dieselben Rechte.

Monatselfchen 1 von Gisela Kibele

Januar

Kalt
und grau
Wälder und Wiesen
Alle Klänge sind verstummt

Winterruhe

Februar

bunt
und grell
Masken beim Tanz
wildes Treiben und Toben

Karneval

März

vielversprechend
erste Blüten
Farben und Klänge
Sonne bringt neues Leben

Frühling

April

Unvorhersehbar
Wolken Sonne
leuchtet im Schatten
Leben steigt ins Licht

Auferstehung

Mai

Verschwenderisch
verteilte Farben
Wärme Vogelgesang Blütenduft
schön ist der Mai

Lebensfreude

Juni

Sonne
im Zenit
warme Winde wehen
Grillen zirpen, Nächte sternenklar

Sommeranfang

Juli

Sommer
Sonne schenkt
Wärme und Licht
lange und helle Tage

Fröhlichkeit

August

brütend
die Hitze
flirrende Luft überall
bald endet der Sommer

Reifezeit

September

Spinnenfäden
schimmern silbern
kreuz und quer
Sonne, Wolken, Wind spielen

Altweibersommer

Oktober

Wolken
ziehen dahin
verdichten sich grau
decken letzte Farben zu

Herbst

November

Welkende
bunte Blätter
fallen zur Erde
Nebel über dem Land

Vergänglichkeit

Dezember

Dunkelheit
brennende Kerzen
Zeit der Stille
Wärme suchen und Licht

Erwartung
Alle Rechte an Texten und Bildern bei Gisela Kibele

Monatselfchen 2 von Kira Stöwe

Januar

Weiß
flockiger Schnee
Schlittschuh auf Eis
Äste schwer und tief

Winter

Februar

Aschermittwoch
Trubel vorbei
Stille und Einkehr
Loslassen - Weniger ist mehr

Fastenzeit

März

Bienen
am Krokus
Neues Leben entsteht
Alle Wesen bekommen Kraft

Aufbruch

April

Regen
Sonne Sturm
Der launische April
macht was er will

Reingelegt

Mai

Mairegen
Wachstum Fruchtbarkeit
Bäume schlagen aus
tanzen jauchzen springen singen

Blütenmeer

Juni

Sonne
leichte Kleidung
Wärme und Licht
Mohn und reifendes Korn

Sommer

Juli

Hitze
kalte Dusche
schwimmen im See
ruhen in der Abendbrise

Urlaub

August

Riesenrad
Buden Menschenmengen
Backfisch Bratäpfel Liebesherzen
strahlende Girlanden und Kinderaugen

Jahrmarkt

September

Altweiberspinnen
laue Luft
der Herbst naht
gehn wir zum Oktoberfest

Leichtigkeit

Oktober

Nebel
erste Kühle
rot gelbe Blätter
Rascheln bei jedem Schritt

Vergehen

November

Trauer
und Tod
verlassen - Tränen allein
Aus Wut wird Liebe

Sehnen

Dezember

Glitzer
und Sterne
überall schon längst
nichts ist wie früher

Rückzug

Quellen

Seite und Texte

Kira Stöwe, Dezember 2013. Kopieren nur nach Anfrage.

Bilder

Die Bilder sind bei commons.wikimedia.org. Die Links zeigen auf die Originalseiten mit Bild, Autor und Rechten. Für meine (Kira Stöwe) Variationen der Bilder gelten dieselben Rechte.

Ich bin

Zum Dokument

Mathematik

 >Persönliches  >Primzahlen  >Graphentheorie  >Abba  >Polytope

Persönliches

Stacheln

Persönliches zu "meiner" Mathematik

Ich (Kira Stöwe) habe Mathematik und Physik studiert, beschäftige mich jetzt aber nur noch mit Mathematik als Hobby. Ich suche aus Neugier nach etwas, das ich noch nicht kenne. Der Weg, das Suchen, ist so wichtig für mich wie das Ziel, etwas zu finden. Dabei will ich nicht davon beeinflusst werden, was andere gefunden haben. Vielleicht sehe ich auf meinem Weg etwas, das auf Standardwegen übersehen wird. Nachträglich schaue ich flüchtig im Internet, was "der Rest der Welt" zu meinen Themen geschrieben hat.

Für mich ist das ein schönes Hobby, ähnlich dem Schatzsuchen. Ich empfehle es auch anderen: Schau, welches Gebiet Dich interessiert, welche Fragen Du dazu hast und suche allein oder mit anderen nach Lösungen. Gerade junge Leute haben wichtige Entdeckungen in der Mathematik gemacht, aber auch ältere können ihre Freude haben und ihr Hirn trainieren.

Primzahlen

Primzahlen sind Zahlen wie 2,3,5,7,11,13,..., die nur durch 1 und durch sich selbst teilbar sind. Es gibt unendlich viele Primzahlen. In der Zahlentheorie (der Theorie ganzer Zahlen) wird ihre Verteilung untersucht.
Vorgesehener Text:
Hier wird dazu ein eigener Weg beschritten. Grafiken zeigen bis 10.000.000 den allgemeinen Verlauf und quasi zu fällige Abweichungen.
Dokument dazu

Graphentheorie

In der Graphentheorie der Mathematik geht es abstrakt um Ecken (auch Knoten genannt), die durch Kanten verbunden sind. Dabei spielt es kaum eine Rolle, was das für Ecken und Kanten sind, sondern nur um die Beziehung.

Vorgesehener Text:
Ebene Graphen mit speziellen Eigenschaften
Dokument dazu

Abba

Vorgesehener Text:
  • Methoden zur fairen Verteilung von Werten oder Aufgaben zwischen zwei Personen
  • Die Folge abba baab baab abba ... bzw. 1,-1,-1,1, ...
  • Eine glatte reelle Funktion, welche für natürliche Zahlen die Werte der Folge annimmt
  • Die Funktion u(x)=∏i=0,1,2,.. (1-x2i) und ihre Darstellung für komplexe Zahlen
  • Erweiterung auf mehr Personen, Folgenwerte (abc bca cab bca ...) und auf eine Entsprechung zu u(x)*u(x)
Dokument dazu

Polytope

Polygone (viele Linien) sind z.B. Dreieck, Viereck, Fünfeck, und Pentagramm.
Polyeder (viele Flächen) sind z.B. Tetraeder, Oktaeder und Würfel.
Polytope (viele Bereiche) sind eine Verallgemeinerung von beidem. Beispiele: Unendliche Polytope wie die Kachelung der Ebene mit Quadraten, Dreiecken oder Sechsecken und die Füllung des Raumes mit Würfeln, ähnliche Objekte in anderen mathemathischen Räumen.
Kira Stöwe hat dazu unabhängig von anderen Mathematikern geforscht. Hier will sie die Theorie und die Schönheit von Polytopen vermitteln. Dazu gibt es bisher folgende Version im Web:

Links zu eigenen Seiten

Deutsch

English

Welcome!

I am Kira Stöwe and live in Cologne/Germany.
Until now there are only the following English pages: