 kira-s
kira-s
Primzahlen
- Vorbemerkungen
- Theorie
- Zahlentheorie
- Prüfen einer Zahl
- Liste vieler Primzahlen
- Quasi zufällig
- Primzahlhäufigkeit
- Erster Eindruck
- Systematik
- Primzahldichte
- Primzahlfunktion
- Begründung
- Variation der Dichte
- Problem
- Lösungen
- Werte für un und vn
- Zetafunktion
- Summen
Vorbemerkungen
| Zielgruppe: | mathematisch interessierte Leute, keine Sezialisten |
| Vorkenntnisse: | Mengen (nur als Begriff), natürliche, ganze und reelle Zahlen und rechnen damit. |
| Ziele: | 1. Grundkenntnisse vermitteln
2. Die Verteilung der Primzahlen so zu verstehen und zu veranschaulichen, dass dabei der allgemeine Verlauf und die quasi zufälligen Schwankungen zu sehen sind. |
| Vorgehen: | Summen berechnen und darstellen |
| benutzte Quelle: | hauptsächlich http://de.wikipedia.org/wiki/Primzahlsatz vom November 2012 |
| Eigenanteil: | Fast alles andere, insbesondere die 2. Zielsetzung und die Berechnungen dazu. Vermutlich gibt es ähnliches schon lange. |
| Fehler | Ich habe die Formeln und Berechnungen nicht gründlich überprüft und vermute Fehler darin. |
Theorie
Primzahlen und Zahlentheorie
Definition: Eine Primzahl ist eine ganze Zahl p>1, die nur durch 1 und sich selbst teilbar ist. Der Buchstabe p wird hier für Primzahlen benutzt.Die Primzahlen bilden eine unendliche Folge p1=2, p2=3, p3=5, p4=7, p5=11, ...
(Beweis: Zu jeder endlichen Menge von Primzahlen ist (1 + deren Produkt) durch keine der Primzahlen teilbar, es gibt also noch mehr.)
Die Zahlentheorie beschäftigt sich großenteils mit natürlichen Zahlen, insbesondere mit Primzahlen: Finden großer Primzahlen und Zerlegung von Zahlen in Primfaktoren (beides wichtig zur Ver- und Entschlüsselung von Texten) und um die Verteilung von Primzahlen (z.B. Wie viele Primzahlen gibt es ≤n?).
Man unterscheidet die elementare Zahlentheorie, welche nur relle Zahlen benutzt und die analytische Zahlentheorie, welche mit komplexen Zahlen weitere Ergebnisse liefert. Hier geht es neben elementarer Theorie vor allem um das experimentelle Auszählen, Summieren und Darstellen.
Prüfen einer Zahl
Um zu prüfen, ob eine Zahl n prim ist, kann man entsprechend der Definition für alle Zahlen k, 1<k<n testen, ob n/k ganz ist. Es reicht aber, für Primzahlen p≤√(n),zu testen, ob n/p ganz ist und nach einer gefundenen aufzuhören. Bei großen Zahlen wird dieses Vorgehen immer aufwändiger. Dann nutzt man andere, komplizierte Tests.Liste vieler Primzahlen, Sieb des Eratosthenes

Bild bei Wikimedia: http://upload.wikimedia.org/wikipedia/commons/d/dc/Animation_schnell_-_Sieb_des_Eratosthenes.gif
Um eine Liste von Primzahen, im Beispiel bis 120, zu erstellen, muss man nicht jede der Zahlen wie eben angegeben prüfen. Viel einfacher geht es mit dem "Sieb des Eratosthenes" . (Wikipedia-Artikel, Kurzinfo zu Eratosthenes). Die Zahlen von 2 bis z.B. 120, werden gelistet. Iterativ wird die kleinste nicht gestrichene Zahl als Primzahl genommen, ihre Vielfachen werden gestrichen. Als Rechenoperation reicht die Addition.
Eratosthenes lebte ca 276-194 v.Chr., vermaß Erde,
Mond, Sonne und Sternzeichen, erklärte Finsternisse,
Wende- und Polarkreise und Winde und leitete die Bibliothek von Alexandria.
Das Verfahren gab es schon vor ihm, aber erst er nannte es Sieb.
Man spart Platz und Arbeit, wenn man nur die ungeraden Zahlen benutzt. So kann man mit einem normalen Computer in kurzer Zeit alle Primzahlen bis 10.000.000.000 finden. Dazu müssen nur die Primzahlen bis 100.000 dauerhaft im Speicher sein.
Quasi zufällige Verteilung
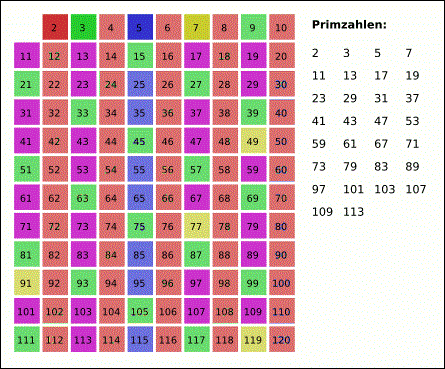
Endstand der Animation des Siebs von Eratosthenes
| Primzahlen | Vielfache davon |
| 2 braun | hellbraun, auf senkrechten Linien |
| 3 grün | hellgrün, 3+6, 3+12,... im Muster |
| 5 blau | hellblau, unter der 5 regelmäßig |
| 7 gelb | hellgelb, im Muster mit Lücken |
| weitere lila, bilden zusammen mit gelben Plätzen ein Muster | keine, 121=11*11 wäre die erste Zahl |
Wenn man die Zahlen einfach hintereinander schreibt,
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
sieht die Verteilung mehr zufällig aus, erst das Rechteck zeigt etwas Ordnung.
Eine solche zufällig aussehende Verteilung mit versteckter Struktur heißt hier "quasi zufällig".
Primzahlhäufigkeit
Erster Eindruck, erste Überlegung

Endstand der Animation des Siebs von Eratosthenes
Im obigen Bild gibt es drei Zeilen mit je vier Primzahlen: 2,3,5,7, 11,13,17,19, 101,103,107,109. Kommt so etwas oft vor? Antwort: nein. Das liegt daran, dass die Primzahlen immer weniger zwischen anderen Zahlen vorkommen. Primzahlzwillinge p,p+2 und Primzahlvierlige werden immer seltener; man weiß in beiden Fällen nicht, ob ihre Anzahl endlich ist.
Die relative Häufigkeit nimmt deshalb ab, weil im Sieb immer mehr Zahlen gestrichen werden und so weniger Plätze für Primzahlen übrig bleiben. Um die Abnahme der Häufigkeit besser zu verstehen, sehen wir genauer hin, was beim Sieb des Eratosthenes passiert.
Systematik
Die folgenden Zeilen zeigen ein Sieb des Eratosthenes für Zahlen bis 2∗30=60.
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
- Anfangs sind alle Zahlen Kandidaten und als solche grau. Das ist hier nicht gezeigt.
- Im ersten Zeilenpaar ist die 2 lila als Primzahl markiert. Gestrichen (schwarz) sind alle Vielfachen von davon: 4=2, 6, 8,... Die Zahlen 4=2∗2 und 5 sind rosa hinterlegt. Das Muster (schwarz, grau) wiederholt sich danach laufend.
- Im zweiten Zeilenpaar ist die erste verliebene Zahl 3 lila als Primzahl markiert. Neu gestrichen (schwarz) sind alle Vielfachen von von 3, die noch nicht gestrichen waren: 9, 15, 21,... Die 6=2∗3 Zahlen ab 9=3∗3 sind rosa hinterlegt, ihr Muster wiederholt sich.
- Im dritten Zeilenpaar ist die erste verliebene Zahl 5 lila als Primzahl markiert. Neu gestrichen (schwarz) sind alle Vielfachen von von 5, die noch nicht gestrichen waren: 25, 35, 55. Die 30=2∗3∗5 Zahlen ab 25=5∗5 sind rosa hinterlegt, ihr Muster wiederholt sich.
- Zur nächsten Primzahl 7 gehört ein Muster der Länge 210=2∗3∗5∗7, das bei 49=7∗7 beginnt. Es überlappt sich also mit dem Muster zur Zahl 5.
Dafür definieren wir eine Häufigkeitsfunktion h(n):
- h(1) = h(2) = h(3) = 1
- h(p²) = h(p²-1)*(1-1/p) für Primzahlen p
(Der Faktor (1-1/p) kommt daher, dass von den bisherigen Kandidaten ein Anteil 1/p gestrichen wird.) - Sonst bleibt h konstant.
Es folgt:
h(p²) = ∏p'<p, prim (1-1/p')
Die Funktion h(p) soll für große Argumente geschätzt werden.
Dazu wir zunächst der Logarithmus gebildet:
ln(h(p²)) = ∑p'<p, prim ln(1-1/p')
Den Logarithmus ln(1-1/p') ersetzen wir durch -1/p':
ln(h(p²)) ≃ c1-∑p'<p, prim 1/p'
Hier ist c1 eine Konstante, welche die Ungenauigkeit in der Gleichung
für große p gegen 0 gehen lässt. c1 ist gegeben durch die
Meissel-Mertens-Konstante M1:
c1 = M1 - ln(2)
M1 = limn→∞ (∑p≤n, prim 1/p - ln(ln(n)) = 0.261 497 212 847 642 783 75...
M1 = limn→∞ (∑p≤n, prim 1/p - ln(ln(n)) = 0.261 497 212 847 642 783 75...
Primzahldichte
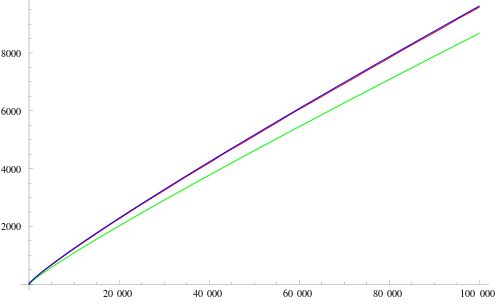
Primzahlfunktion
(Das Wort Primzahldichte bedeutet bei der Quelle in Wikipedia π(x)/x und wird hier anders benutzt.)
Die Primzahlfunktion π(x) gibt an, wieviele Primzahlen es bis zu der reellen Zahl x gibt:
π(x)=∑p≤x 1
π(x) ist eine Stufenfunktion, springt bei jeder Primzahl um 1, sieht aber im Bild (rot) wegen des Maßstabes glatt aus. Es gibt glatte Näherungsfunktionen S(x), ihre Ableitung ist die Primzahldichte s(x).
Die Näherung x/ln(x) (grün) wurde 1793 von Carl Friedrich Gauß im Alter von 15 Jahren gefunden. Wir benutzen im folgenden die bessere Näherung
S(x)=Li(x)=∫2..xdt/ln(t)
(blau). Dabei ist also die Primzahldichte s(x)=1/ln(x). Für beide Näherungen gilt limx→∞(π(x)/S(x))=1.
Begründung der Funktion s(x)=1/ln(x)
Die Dichte s(x)=1/ln(x) lässt sich aus der Häufigkeitsfunktion h herleiten:Für die Häufigkeit h(x) wurde auf der vorigen Seite geschrieben:
ln(h(p²)) ≃ c1-∑p'<p, prim 1/p'
Wir nehmen an, dass s(x)≃h(x) ist, ersetzen die Funktion h durch
die Funktion s, setzen x:=p² und ersetzen ∑p'<p,prim
durch ∫t≤√x s(t) dt.
ln(s(x)) ≃ c2-∫t≤√(x) s(t)/t dt
(Bei dem Integral ist kein Anfangswert für t angegeben, es wird eine
beliebige Stammfunktion benutzt und die Konstante c2 geeignet gesetzt.)
Differenzieren nach x gibt
s'(x) / s(x) ≃ - s(√x) / 2x
s'(x) ≃ - s(x) s(√x) / 2x
Dies wird als Gleichung von der Funktion s(x)=1/ln(x) erfüllt.
Sie ist wohl die wichtigste Formel für die Primzahldichte.
Im nächsten Kapitel geht es um weitere Lösungen der Gleichung.
s'(x) ≃ - s(x) s(√x) / 2x
Warnung: Das Zeichen ≃ bedeutet "asymptotisch gleich". Das Differenzieren einer solchen Formel kann zu Fehlern führen. Bei s(x)=1/ln(x) und weiteren Funktionen des nächsten Kapitels stimmt das Ergebnis aber. Es gilt vermutlich nicht für die dort angedeutete unendliche Reihe solcher Funktionen. Trotzdem kann dafür noch die Formel vor dem Differenzieren gelten.
Variation der Dichtefunktion
Dieses Kapitel ist relativ schwer zu verstehen und benutzt auch komplexe Zahlen. Die Überlegungen stammen vom Autor. Es bleiben wesentliche Fragen und die Verwertbarkeit offen. Am Ende wird ein Vergleich mit Riemans Arbeit versucht.Problembeschreibung und eine Gleichung dazu
Wenn die Primzahldichte anfangs von 1/ln(x) abweicht, gibt das Änderungen bei x2, x3, x4,... Solche Abweichungen werden hier behandelt, allerdinges nur als eine relativ kleine, glatte Funktion r(x). (Anzeichen für schnelle Schwankungen ergeben sich daraus gegen Ende des Kapitels.)s(x) = (1/ln(x)) (1+r(x))
|r(x)|<<1
Das setzen wir in die Gleichung für s' ein:
|r(x)|<<1
s'(x) ≃ - s(x) s(√x) / 2x
d/dx ((1+r(x))/ln(x)) ≃ - ((1+r(x))/ln(x)) ((1+r(√x))/ln(√x)) / 2x
Quadrate in r werden ignoriert. Teile ohne r(x) und r'(x):=dr/dx heben
sich weg. Es bleibt:
d/dx ((1+r(x))/ln(x)) ≃ - ((1+r(x))/ln(x)) ((1+r(√x))/ln(√x)) / 2x
r'(x)/ln(x) - r(x)/x(ln(x))² ≃ - (r(x)+r(√x)+r(x)r(√x)) / (x(ln(x))²)
r'(x) ≃ - r(√(x))(1+r(x)) / (x ln(x))
Wegen |r(x)|<<1 entfällt das Quadrat in r:
r'(x) ≃ - r(√(x))(1+r(x)) / (x ln(x))
r'(x) = - r(√(x)) / (x ln(x))
(Wir schreiben nach Weglassen der Quadrate = statt ≃, denn solche Lösungen suchen wir.)
Verschiedene Lösungen dieser in r linearen Gleichung können kombiniert werden.
Lösungen der Gleichung
Zum Suchen von Lösungen zu der Gleichung r'(x) = - r(√(x)) / (x ln(x)) setzen wir t:=ln(ln(x)), ρ(t):=r(x) und ρ':=dρ/dt. Aus der Gleichung für r' wird eine für ρ', die unabhängig von t ist! Als Ansatz benutzen wir eine Exponentialfunktion.ρ'(t) = -ρ(t-ln 2)
ρ(t) = exp(k t)
k exp(k t) = -exp(k(t-ln 2)) = -exp(k t) * exp(-k ln 2)
k = -exp(-k ln 2) = -2-k
k+2-k=0
ρ(t) = exp(k t)
k exp(k t) = -exp(k(t-ln 2)) = -exp(k t) * exp(-k ln 2)
k = -exp(-k ln 2) = -2-k
k+2-k=0
Es gibt keine reelle Lösung dazu (k+2-k ist immer positiv). Mit einem Computer-Suchlauf wurde aber eine Serie komplexer Lösungen gefunden, die anscheinend unendlich ist:
für n=0,1,2,..: kn=un±vni (un<0, vn>0)
Jedes Paar ergibt zwei reelle Anteile zu ρ(t):
ρn(t) = exp(un t) (an cos(vn t) + bn sin(vn t))
Sie sind gedämpfte Schwingungen, wie sie in der Mechanik vorkommen.
Jede erfüllt die obigen Bedingung: klein und glatt. Das gilt auch für
die Summe endlich vieler Anteile. Für n→∞ werden die
Wellenlängen immer kleiner, und ∑n=0..∞ ρn(t) muss
nicht mehr glatt sein, kann vielleicht die quasi zufällige Verteilung
der Primzahlen widergeben. Aber dazu müsste man erst die Koeffizienten
an und bn kennen.
Da dem Autor die Theorie dazu fehlt, schägt er vor, einige Koeffizienten an ein Anfangsstück der Primzahlen anzupassen. Dazu minimiert man die folgende gewichtete Quadratsumme:
∑p≤pmax, prim ((h(p²)-s(p²))² g(p²))
mit (s. Primzahlhäufigkeit)
h(p²) = ∏p'<p, prim (1-1/p') oder
h(p²) = exp(c1-∑p'<p, prim 1/p')
Die Gewichtsfunktion g(p²) wird so gewählt, dass sie bei verschiedenen pmax
ähnliche Ergebnisse liefert. Dann sieht man, ob das ganze einen Sinn hat.
Werte für un und vn
| n | u geschätzt u berechnet |
v geschätzt v berechnet |
|---|---|---|
| 0 | -0.71197156072 -0.82467854614 | 1.51480162529 1.56743212385 |
| 1 | -3.51649200245 -3.51523672192 | 10.88498759840 10.88005320845 |
| 2 | -4.36174430094 -4.36143141283 | 20.08790781839 20.08716280600 |
| 3 | -4.88897686608 -4.88885664543 | 29.22132926521 29.22118550826 |
| 4 | -5.27390661314 -5.27384865880 | 38.32779425793 38.32778722878 |
| 5 | -5.57739256242 -5.57736047492 | 47.42084746235 47.42087628105 |
| 6 | -5.82799035618 -5.82797084936 | 56.50619180820 56.50622856080 |
| 7 | -6.04143891129 -6.04142622483 | 65.58666808405 65.58670420570 |
| 8 | -6.22734809744 -6.22733941446 | 74.66385932555 74.66389226609 |
| 9 | -6.39202055346 -6.39201436790 | 83.73872155728 83.73875079734 |
| 10 | -6.53981500564 -6.53981045480 | 92.81186822494 92.81189393786 |
| 100 | -9.82778052821 -9.82778052513 | 908.72260613845 908.72260638422 |
| 1000 | -13.14640859939 -13.14640859939 | 9066.98437193252 9066.98437193332 |
| 10000 | -16.46801096853 -16.46801096853 | 90649.4687545248 90649.4687545248 |
| 100000 | -19.78990658388 -19.78990658388 | 906474.294514013 906474.294514013 |
| 1000000 | -23.11183143242 -23.11183143242 | 9064722.54983078 9064722.54983078 |
| 10000000 | -26.43375920270 -26.43375920270 | 90647205.1027235 90647205.1027235 |
| 100000000 | -29.75568726512 -29.75568726512 | 906472030.631619 906472030.631619 |
| 1000000000 | -33.07761535676 -33.07761535676 | 9064720285.92057 9064720285.92057 |
Die Schätzung ist:
h := 2 π (n+1/4) / ln(2) (ungefährer Wert von v)
v := h - ln(h) / ((ln(2)² h) (genauerer Wert von v)
u := -ln(v)/ln(2) - 1.50139 ln(v)²/v²
Die Zahl 1.50139 ist ohne Bedeutung angepasst.
v := h - ln(h) / ((ln(2)² h) (genauerer Wert von v)
u := -ln(v)/ln(2) - 1.50139 ln(v)²/v²
Vergleich mit der Zetafunktion
Gibt es irgendeinen Zusammenhang mit den Nullstellen der Zetafunktion?Im Gegensatz zur Zetafunktion sind die Nullstellen hier plausibel: Bei jedem Zyklus von exp(-ln(2)i v) gibt es genau einen Schnitt mit der Ebene k. Es gibt keine weitere Nullstellen von k+2k.
Summen
Als Verallgemeinerung der Primzahlfuntion π(x)=∑p≤x 1 untersuchen wir SummenF(x)=∑p≤x g(x).
Im Falle g(x)=1 ist F(x)=π(x). Die Gewichtsfunktion g(x) soll normalerweise das Übergewicht der großen Zahlen in der Summe reduzieren.
Eine Näherung zu F(x) ist
T(x):=∫2..x(s(x)∗g(x) dt) + c
Dabei ist c eine Konstante, die Unregelmäßigkeiten bei kleinen Zahlen ausgleicht, um die Näherung bei großen Zahlen zu verbessern.
Wenn das Integral aufwändig zu berechnen ist, kann eine Näherung benutzt werden, bei der die relative Differenz =O(1/x) ist.
Es wird wie bei π(x) angenommen, dass limx→∞(F(x)/T(x))=1 ist, oder gleichwertig, dass die Funktion
D(x):=F(x)/T(x) - 1
gegen 0 geht. Um noch etwas zu sehen, wird D(x) mit einer "Vergrößerung" v(x) multipliziert und dann abgebildet.
Die Berechnugen werden für alle Zahlen x<10.000.000.000 gemacht. Als Ordinate in den Darstellungen ist die Zahl x wenig geeignet, da man dabei das Verhalten bei kleinen x-Werten nicht sieht. Statt dessen wird
x1:=ln(x)
oder
x2:=ln(ln(x))
benutzt. Umgekehrt ist x1=exp(x2) und x=exp(x1)=exp(exp(x2)).
Folgende Fälle werden berechnet:
- g(x)=1, T(x)=Li(x), v(x)=x2*√(x)
- g(x)=1/x, T(x)=x2+M1, v(x)=x1*x2*√(x)