Graphentheorie
- 1.1 Graphen
- 1.2 Ebene Graphen
- 1.3 Zusammenziehen von Kanten und Homomorphie - trennende Kreise in Dreiecksgraphen
- 2.1 Bekanntes
- 2.2 Mein Beitrag
- 2.3 Mein Weg
- 3.1 Bekanntes
- 3.2 Mein Beitrag
- 3.3 Mein Weg
Graphen
- In der Graphentheorie der Mathematik geht es abstrakt um Ecken (auch Knoten genannt), die durch Kanten verbunden sind. Dabei spielt es kaum eine Rolle, was das für Ecken und Kanten sind, sondern nur um die Beziehung.
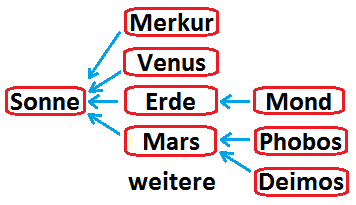
- Ein Beispiel mit gerichteten Kanten ist das Sonnensystem mit Sonne, Planeten und Monden als Ecken und dem Bezug "kreist um".
- Bei der Verwandschaft von Personen ist die Beziehung Elternteil->Kind gerichtet. Die Beziehung Partner--Partner (ehelich oder eingetragen) ist ungerichtet.
- Im folgenden sollen die Graphen immer endlich sein. Ihre Kanten sollen ungerichtet sein, zwei verschiedene Ecken haben und nicht mehrfach bei demselben Eckenpaar sein.
- Ecken, die durch eine Kante verbunden sind, werden auch Nachbarn genannt.
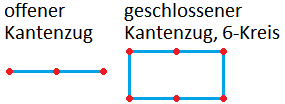
- Kantenzüge: s. Bild. Es sollen keine Ecken doppelt vorkommen. Geschlossene Kantenzüge werden auch Kreise ganannt. Die Bezeichnung 6-Kreis ist von mir.
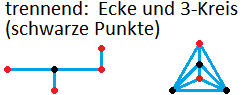
- Eine Teilmenge T von Ecken eines Graphen trennt diesen, wenn es Paare von Ecken (nicht in T) gibt, die nur über Kantenzüge durch T verbunden sind. Im folgenden werden insbesondere trennende Kreise behandelt.
Ebene Graphen
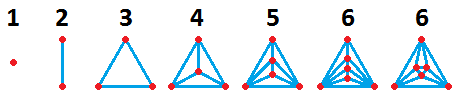 Dabei werden vollständige Graphen (bei denen man in der Ebene
ohne zusätzliche Ecken keine Kanten mehr hinzufügen kann) zu Dreiecksgraphen (Alle Flächen sind
Dreiecke. Dazu muss der Graph natürlich mindestens 3 Ecken haben.).
Dabei werden vollständige Graphen (bei denen man in der Ebene
ohne zusätzliche Ecken keine Kanten mehr hinzufügen kann) zu Dreiecksgraphen (Alle Flächen sind
Dreiecke. Dazu muss der Graph natürlich mindestens 3 Ecken haben.).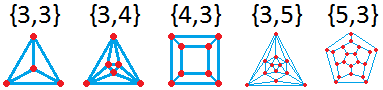 Indem man einen Dreiecksgraphen auf die Kugel projziert, sie dreht und dann
zurück projiziert bekommt man einen isomorphen Dreicksgraphen, bei dem ein
beliebiges Dreieck außen ist. Ebenso kann man die Ecken und Kanten eines Körpers
nach außen auf eine Kugel projizieren und weiter in die Ebene. Das Bild zeigt
die 5 Platonischen Körper: Tetraeder, Oktaeder, Würfel, Ikosaeder und
Dodekaeder. (Die geschweiften Klammern sind Schläffli-Symbole mit der Zahl der Ecken pro Fläche und der Zahl der Flächen pro Ecke.)
Indem man einen Dreiecksgraphen auf die Kugel projziert, sie dreht und dann
zurück projiziert bekommt man einen isomorphen Dreicksgraphen, bei dem ein
beliebiges Dreieck außen ist. Ebenso kann man die Ecken und Kanten eines Körpers
nach außen auf eine Kugel projizieren und weiter in die Ebene. Das Bild zeigt
die 5 Platonischen Körper: Tetraeder, Oktaeder, Würfel, Ikosaeder und
Dodekaeder. (Die geschweiften Klammern sind Schläffli-Symbole mit der Zahl der Ecken pro Fläche und der Zahl der Flächen pro Ecke.)1.3 Zusammenziehen von Kanten und Homomorphie - trennende Kreise in Dreiecksgraphen
- Jeder Dreiecksgraph D außer dem Dreieck und dem Tetraeder enthält mindestens ein trennendes Dreieck, Viereck oder Fünfeck.
- Wenn eine Kante nicht auf einem trennenden Dreieck liegt, kann man sie "zusammenziehen". Das heißt, man ersetzt die Kante k mit den Knoten a und b durch einen Knoten c und verbindet c mit allen anderen Nachbarn von a und b. Das Ergebnis ist wieder ein Dreiecksgraph D'.
- Wenn D kein trennendes Dreieck enthält und eine Kante k nicht auf einem trennenden Viereck liegt und man sie zusammenzieht, enthält D' auch kein trennendes Dreieck.
- Wenn D kein trennendes Dreieck und kein trennendes Viereck enthält und eine Kante k nicht auf einem trennenden Fünfeck liegt und man sie zusammenzieht, enthält D' auch kein trennendes Dreieck oder trennendes Viereck.
 In der Graphentheorie der Mathematik geht es abstrakt um Ecken
(auch Knoten genannt),
die durch Kanten verbunden sind. Dabei spielt es kaum eine Rolle,
was das für Ecken und Kanten sind, sondern nur um die Beziehung.
Ein Beispiel mit gerichteten Kanten ist das Sonnensystem mit Sonne, Planeten
und Monden als Ecken und dem Bezug "kreist um". Im folgenden sollen die Graphen
immer endlich sein und ihre Kanten sollen ungerichtet sein, zwei verschiedenen
Ecken haben und nicht mehrfach bei demselben Eckenpaar sein. Ecken,
die durch eine Kante verbunden sind, werden auch Nachbarn genannt.
In der Graphentheorie der Mathematik geht es abstrakt um Ecken
(auch Knoten genannt),
die durch Kanten verbunden sind. Dabei spielt es kaum eine Rolle,
was das für Ecken und Kanten sind, sondern nur um die Beziehung.
Ein Beispiel mit gerichteten Kanten ist das Sonnensystem mit Sonne, Planeten
und Monden als Ecken und dem Bezug "kreist um". Im folgenden sollen die Graphen
immer endlich sein und ihre Kanten sollen ungerichtet sein, zwei verschiedenen
Ecken haben und nicht mehrfach bei demselben Eckenpaar sein. Ecken,
die durch eine Kante verbunden sind, werden auch Nachbarn genannt.
Ebene Graphen
Hier geht es um ebene Graphen. Dabei sind die Ecken Punkte in der Ebene und die Kanten Verbindungslinien. Die Kanten kreuzen sich nicht und der Graph ist zusammenhängend (Zwischen je 2 verschiedenen Ecken gibt es einen Kantenzug.). Folgendes ist bekannt und einleuchtend:- Bei jedem ebenen Graphen lassen sich die Ecken so verschieben und die Kanten so biegen, dass alle Kanten gerade werden.
 Dabei werden vollständige Graphen (bei denen man in der Ebene
keine Kanten mehr hinzufügen kann) zu Dreiecksgraphen (Alle Flächen sind
Dreiecke. Dazu muss der Graph natürlich mindestens 3 Ecken haben.).
Dabei werden vollständige Graphen (bei denen man in der Ebene
keine Kanten mehr hinzufügen kann) zu Dreiecksgraphen (Alle Flächen sind
Dreiecke. Dazu muss der Graph natürlich mindestens 3 Ecken haben.).- Das Schieben und Biegen von (1.) gibt eine isomorphe Abbildung (eine Zuordnung der Ecken zweier Graphen, bei der die Verbindungen erhalten bleiben).
- Jeder ebene Graph kann isomorph auf einen Graphen auf der Kugeloberfläche abgebildet werden. (Dazu legt man die Kugel auf die Ebene und projiziert in Richtung des Punktes, der dem Berührungspunkt gegenüber ist.)
 Indem man einen Dreiecksgraphen auf die Kugel projziert, sie dreht und dann
zurück projiziert bekommt man einen isomorphen Dreicksgraphen, bei dem ein
beliebiges Dreieck außen ist. Ebenso kann man die Ecken und Kanten eines Körpers
nach außen auf eine Kugel projizieren und weiter in die Ebene. Das Bild zeigt
die 5 Platonischen Körper: Tetraeder, Oktaeder, Würfel, Ikosaeder und
Dodekaeder.
Indem man einen Dreiecksgraphen auf die Kugel projziert, sie dreht und dann
zurück projiziert bekommt man einen isomorphen Dreicksgraphen, bei dem ein
beliebiges Dreieck außen ist. Ebenso kann man die Ecken und Kanten eines Körpers
nach außen auf eine Kugel projizieren und weiter in die Ebene. Das Bild zeigt
die 5 Platonischen Körper: Tetraeder, Oktaeder, Würfel, Ikosaeder und
Dodekaeder.- Ein Kreis (Dreieck, Viereck, ...) ist eine geschlossene Kantenfolge
ohne Dopplungen. Ein trennender Kreis ist ein Kreis, bei dem innen und
außen weitere Ecken sind.
Dabei trifft jede Kantenfolge zwischen innen und außen den trennenden Kreis. - Im Dreiecksgraphen lässt sich jede Kante, die nicht auf einem trennenden Dreieck liegt, zusammenziehen. Dabei entsteht ein neuer Graph, bei dem die beiden Ecken durch eine ersetzt sind. Sie ist mit allen ursprünglichen Nachbarn verbunden. Das Ergebnis ist wieder ein Dreiecksgraph. Ausnahme: Das Dreieck wird zu einem Graphen mit zwei Ecken.
- Eine (Ecken-)Färbung eines Graphen mit n Farben ist eine Abbildung
der Ecken auf eine Menge mit n Elementen, den Farben. Hier werden nur
Färbungen behandelt, bei denen Nachbarn verschieden gefärbt sind.
Eine alte Vermutung war: Jeder ebene Graf lässt sich mit maximal 4 Farben färben. Erst nach Jahrhunderten wurde sie mit Hilfe eines Computers als Vierfarbensatz bewiesen. Die Mathematiker suchen noch nach einem Beweis, der von einem Menschen nachvollzogen werden kann.
Zum Beweis reicht es, den Satz für alle Dreiecksgraphen zu beweisen. Begründung: Jeder ebene Graph lässt sich durch weitere Kanten zu einem Dreiecksgraphen erweitern. Wenn der gefärbt ist, ist es der urspüngliche Graph auch.
Graphen mit speziellen Eigenschaften
In einem Seminar zur Graphentheorie bei Prof. Klaus Wagner habe ich die Doktorarbeit von Kais Al-Wahabi (Universität zu Köln 1965) vorgetragen. Sie lautet "Primität und Homomorphie von ebenen Dreiecksgraphen" und ist 1965 veröffentlicht bei Mathematische Annalen Band 161, 327-348 (Link 327 wählen). Die wesentlichen Ergebnisse sind:- Nur beim Oktaeder gibt es kein trennendes Dreieck und jede Kante liegt auf einem trennenden Viereck.
- Jeder größere Dreiecksgraph D ohne trennendes Dreieck lässt sich durch Zusammenziehen von Kanten schrittweise auf den Oktaeder reduzieren.
- Das funktioniert auch, wenn zwei beliebige nicht benachbarte Ecken von D gewählt werden und deren Kanten nicht zusammengezogen werden dürfen.
- Indem man die beiden Ecken im Raum durch eine Kante verbindet gibt es Folgerungen für gewisse nicht ebene Graphen.
Mein Beitrag
Mich interessierten nur die Ergebnisse (1.) und (2.), Prof. Wagner vor allem die Ergebnisse (3.) und (4.). Ich stellte mir die Frage: Lassen sich (1.) und (2.) auf größere Zahlen übertragen?Da jeder Dreiecksgraph mit mehr als 4 Ecken mindestens ein trennendes 3-, 4- oder 5-Eck hat, blieb nur die Übertragung auf Dreiecksgraphen ohne 3- und 4-Ecke. Die Untersuchung war wesentlich aufwändiger als die oben geschilderte Arbeit. Ergebnisse:
- Beim Ikosaeder gibt es kein trennendes 3- oder 4-Eck und jede Kante liegt auf einem trennenden 5-Eck. Das gilt aber auch für zwei weitere Mengen A und B von Dreiecksgraphen (s.u.).
- Jeder größerer Dreiecksgraph D ohne trennende 3- und 4-Ecke lässt sich durch Zusammenziehen von Kanten schrittweise darauf reduzieren.
Ich hatte die Untersuchung ohne Absprache mit Prof. Wagner gemacht. Er sagte, er sei sehr angetan von der Arbeit. Wenn ich auch den Punkt (3.) erledigte, sei das genug für eine Doktorarbeit. Ich fand, ich hatte schon viel mehr geleistet als zu der ersten Doktorarbeit nötig war und hatte keine Lust zu dem dritten Punkt. Eine Promotion im 5. Studiensemester war zwar verlockend (Das ging damals noch ohne Studienabschluss.), aber eigentlich wollte ich Abschluss und Promotion in Physik. Inzwischen finde ich meine Unterlagen nicht mehr.
Vierfarbensatz
Einleitung
Diese Einleitung verwendet Informationen von http://de.wikipedia.org/wiki/Vierfarbensatz.Wie viele Farben braucht man für eine politische Landkarte? Dabei bekommt jedes Land eine Farbe, und Länder mit gemeinsamer Grenzlinie haben verschiedene Farben. Kartographen viel auf, dass sie normalerweise mit 4 Farben auskommen können. Nur wenn Länder aus mehreren Teilen bestehen (Exklaven, Kolonien) waren manchmal mehr Farben erforderlich. Deshalb stellte 1852 Francis Guthrie die Vermutung auf, dass bei allen Landkarten mit zusammenhängenden Ländern vier oder weniger Farben ausreichen.
Es gab viele vergebliche Versuche für einen Beweis oder für ein Gegenbeispiel. Erst 1976 gab es einen ersten Beweis, und man spricht jetzt vom Vierfarbensatz. Der Beweis benötigte aber einen Computer, der eine Vielzahl noch offener Fälle systematisch überprüfte. 2004 gab es den ersten formalen Beweis, der aber auch von einem Computer benötigte. Es wird weiter nach einem Beweis gesucht, der allein von Menschen geführt wird.
Vereinfachung der Frage
Die Frage ist zunächst: "Ist jede Landkarten mit zusammenhängenden Ländern mit 4 oder weniger Farben färbbar?" Diese Frage wird in ein paar Schritten vereinfacht:- Zunächst will man die oft krummen, unübersichtlichen Grenzen der Länder loswerden. Das geschieht durch Umformung in einen ebenen Graphen. Jedem Land entspricht ein Knoten, und die Knoten angrenzender Länder werden miteinander verbunden. Die Frage ist danach: "Ist jeder ebene Graph mit 4 oder weniger Farben färbbar?"
- Dann will man die vielen Formen ebener Graphen loswerden. Bekanntlich lassen sich die Kanten begradigen. Dann werden zusätzliche Kanten eingefügt, so dass man einen Dreiecksgraph erthält. Wenn man diesen färbt, ist damit auch der ursprünliche Graph gefärbt. Somit blöeibt die Frage: "Ist jeder Dreiecksgraph mit 4 oder weniger Farben färbbar?"
- Wenn die Antwort "nein" ist, muss es einen Dreiecksgraphen minimaler Eckenzahl geben, der mindestens 5 Farben braucht. Einen solcher wird jetzt Min-Graph genannt. Die Frage lautet: "Gibt es einen Min-Graph?"
- Jetzt sollen die Typen von Dreiecksgraphen eingeschränkt werden. Ein Dreiecksgraph mit einem trennenden Dreieck kann kein M-Graph sein. Denn man kann den Innenbereich und den Außenbereich unabhängig voneinander färben und beide Färbungen aneinander passen. Wenn jeweils 4 Farben ausreichen, ist der gesamte Graph mit 4 Farben gefärbt. Mit nur etwas mehr Aufwand lässt sich zeigen, dass ein Graph mit trennendem Viereck kein Min-Graph ist. Die Frage bleibt: "Gibt es einen Min-Graph ohne trennende 3- und 4-Ecke?"
Mein Beitrag
Wiederholung der Frage: "Gibt es einen Min-Graph ohne trennende 3- und 4-Ecke?"Zur Beantwortung benutze ich meine obigen Ergebnisse und finde:
- Für den Ikosaeder kann man leicht eine Färbung mit 4 Farben angeben.
- Dasselbe gilt für alle Graphen vom Typ A.
- Die Graphen vom Typ B sind keine Min-Graphen. Begründung: Ich beginne mit dem 3-eck-5-eck-Graph, setze in jedes echte Fünfeck einen Knoten und verbinde sie mit den 5 Knoten auf dem Rand. Wenn es dazu eine 4-Färbung gibt, sind die Fünfecke alle mit 3 Farben gefärbt. Ich ersetze die eingefügten Knoten durch die Ikosaeder-Teile passe deren Färbung an den Rand an und erhalte einen Dreiecksgraphen, der mit 4 Farben gefärbt ist.
- Es bleibt die Frage: "Gibt es einen Min-Graph ohne trennende 3- und 4-Ecke m,it einem trennenden Fünfeck?"
- Zur Verneinung dieser Frage sollen alle Fallunterscheidungen aus Satz 1 untersucht werden. Wenn in jedem Fall aus einer 4-Färbung des Graphen nach dem Kantenzusammenzug ein 4-Färbung des Originals erzeugt werden kann, ist die Frage zu Verneinen. Dann ist der Vierfarbensatz bewiesen.