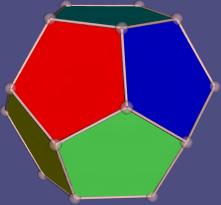
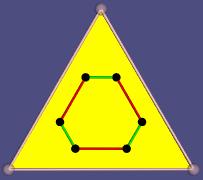
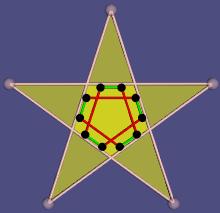
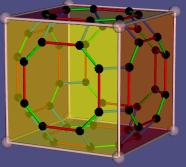
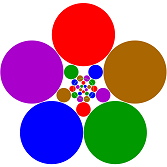
Abstract
This article is based on abstract polytopes as described in the book
"Abstract Regular Polytopes" by Peter McMullen and Egon Schulte.
But an alternative, more flexible definition of realizations is used here.
The usual realization of an abstract cube {4,3} in space only uses
8 points in the space. The new one can do the same but also the solid cube,
the hollow cube, a box open at one side, 8 circles in the plane
and other versions. These all can be distinguished in an abstract way.
Realizations of infinite 4- and 5-polytopes in the plane and in the 3-space
are used for visualizations. Their beauty may get the interest of persons
who never would look at a mathematical paper.
This article primarily is written for experts in the theory opf polytopes.
But other people are invited to read it too, some help texts are given.
What you should know
The term (geometrical) polytope is a generalization of polygon (triangle, rectangle, ...) and poyhedron (three dimensional solid figures with plane borders) to objects in mathematical spaces of other dimensions and types. Polytopes have a dimension n and border elements (called faces) of rank 0 to n-1.
The faces build a partially ordered set (poset). When we look at the posets and ignore the space, we get abstract polytopes. And we get further abstract polytopes as posets with similar properties. Often they can be transformed to mathematical spaces to get new geometrical polytopes. This transformation is called realization.
What is new in this article?
The usual realization in a space only gives points and the information, how they are combined in the other faces. That may satisfy many mathematicians but not me. Hence I define another, more flexible type of realization. It can give not only the eight vertices of a cube but also the solid cube, the hollow cube and other versions.
I use my realization in mathematical spaces normaly not used for polytopes. Such realizations of up to five dimensional abstract polytopes can be visualized. The beauty of the visualization may get the interest of especially young persons who never would look at a mathematical paper.
The author
Kira Stöwe in Cologne, Germany, has studied mathematics and physics. She published in theoretical physics and some other fields. Now she researches in mathematical fields for her pleasure, mostly without contact to literature or other peoples. Only seldom she looks what other persons have found and adepts their terms. Results that she does not find elsewhere may be new or overseen. So she describes her results here and looks for a partner for a scientific publication. In addition she wants to communicate the whole theory in a simple way to children and looks for partners.
Searching polytopes
On leave in 1988 Kira asked herself:
"Euclid showed that there are exactly 5 regular convex polyhedra, the platonic solids. But which objects are there in higher dimensions?"
After some days she had the answer: (6,3,3,..) in (4,5,6,..) dimensions.
Her interest for regular geometric objects grew, and for years she searchd for more. She recognized tessalations of euklidean spaces as polytopes: {∞}, {4,4}, {3,6}, {6,3}, {4,3,..,4}. She found the 9 finite regular polyhedra with skew faces and found polytopes in elliptic, hyperbolic, extended hyperbolic and conformal spaces.
She made a definition equivalent to what is call abstract polytotopes, but formulated as face graphs and flag graphs, defined realizations (not equivalent to the usual ones) and made algorithms, software and images thereto.
The Author
Kira Stöwe ...
- is a woman in Cologne, Germany
- has studied mathematics and physics
- published mainly in theoretical physics
- now researches in mathematical fields for her pleasure,
mostly without contact to literature or other peoples
- starting from the platonic solids found many types of polytopes
which, as she later noticed, were found by others too
- but also dicovered some results that she did not found elsewhere
- describes the results here and looks for a partner for a scientific
publication
- wants to communicate the whole theory in a simple way to children
and looks for partners
Searching polytopes
Kira Stöwe ...
- on leave in 1988 asked herself:
"Euclid showed that there are exactly 5 regular convex polyhedra,
the platonic solids.
But which objects are there in higher dimensions?"
- in a week found the answer (6,3,3,..), but wanted more regular objects
- had years of searching nearly without input from literature or other
persons,
later read of the results of others and adepted their terms
- recognized infinite tessalations of spaces as such objects:
in euklidean spaces {∞}, {4,4}, {3,6}, {6,3}, {4,3,..,4}
in elliptic spaces by identifying opposite elements of the latter ones
in hyperbolic spaces (first seen in graphics by M.C.Escher)
at the end also in extended hyperbolic spaces and in conformal spaces
- found 9 finite regular polyhedra with skew faces,
but did not recognize Petrie's correspondency to the 9 platonic and
Kepler-Poinsot polyhedra
- being familiar with graph theory made a theory of face graphs and flag graphs
which is equivalent to the definition of abstract polytopes later read
in [1]
- defined regularity equivalent to the usual one and realization not
equivalent to the usual one
- discovered extensions to hyperbolic spaces and read of conformal spaces
- found polytopes in extended hyperbolic spaces (hyperideal polytopes)
and their projections in conformal spaces
giving (n-2)-dimensional realizations of n-dimensional abstract
polytopes
- made colored images of these realizations and showed them at kira-s.de
and at exhibitions
Kira Stöwe has studied mathematics and physics. She published in theoretical physics and some other fields. Now she researches in mathematical fields for her pleasure, mostly without contact to literature or other peoples. On leave in 1988 she asked herself: "Euclid described the 5 platonic solids and showed that there are no more such objects. But which objects are there in higher dimensions?" In short she had the answer: 6 in 4 dimensions and 3 for every higher dimension. Her interest for regular geo
metrical objects grew. She found them in lower dimensions (-1 to 2), in tessalations of the plane {4,4}, {3,6}, {6,3}, of higher Eucliden spaces {4,3,..,4} and - by graphics of M.C.Escher - of the hyperbolic plane.
Known topics
The reader should be aquainted with the following topics:
- Mathematical logic, quantors
- Set theory
- Groups
- Generating subset of a group
- Group action
- Linear algebra
- Definition
- Matrices
- Eigenvalues aund -vectors of symmetric matrices
- Partial orders
- Projections and reflections
- Reflections at circles of the plane and of the sphere
- Transformation of a sphere to a plane:
orthogonal, mid point centered, pole centered, mercator
- Geometric spaces
- Euclidean spaces
- Elliptic spaces
- Hyperbolic spaces
- Projective geometry
- Conformal geometry
- Convex polytopes
- Abstract polytopes
- Definition
- Regularity
- Coxeter Groups
- Representation of universal regular polytopes
- Realization
Topics
-
- Another definition of realization of an abstract polytope
- The usual definition of the realization of an abstract polytope P
into an euclidean space E is given by a function
β0:F0→E of the vertices into E
and recursively for i=1..n and f∊Fi:
βi(f)={βi-1(g) | g∊Fi-1∧g≤f}
We call this definition ∊realization and retrict it to faithful
realizations, that is all fi are injective.
- The new Definition uses ⊂ instead of ∊.
In the following the word realization means the new ⊂realization.
- To each ∊realization of a lattice polytope corresponds a
definite ⊂realization. But there are further ⊂realizations.
- To each realization of a polytope corresponds a realization of the
dual.
- A polytope of range n may have realizations of dimension n-2.
- The different realizations of an abstract polytope P can be
characterized in an abstract way.
- Realizations in unusual spaces
- Extended hyperbolic spaces
- Conformal spaces
- Visualzation of realizations
- Calculation of a representation
- Projections
- Aesthetics
Symmetry spaces
All spaces that usually are used for polytopes have a set of points and symmetries. So I abstract:
Definition
- A symmetry space is a pair (M,S) of a set M and
of+ a set S of bijections M→M that form a group.
- The elements are called points and (space-)symmetries.
,
,
Experimental content not used elsewhere in this article:
,
,
,
fixpoints (x is a fixpoint :⇔ ∀
s∊S s(x)=x),
orbit (orbit(x,s), Orbit(M',S'))
corunners (x,y are corunners :⇔ ∀
s∊S (s(x)=x ⇔ s(y)=y),
bunch (pulk: a class of corunners in an S-orbit),
S-orbitclass (orbit in the same class, if they have corunners),
poset of subspaces
Isomorphims and homomorphisms
Definitions:
- A isomorphism/homomorphism
from space (M,S) to space (M',S') is a bijective/surjective
function f:M→M' and a bijective/surjective function g:S→S' with
∀s∊S g(s)={(f(a),f(b))|(a,b)∊s}
- An automorphism in (M,S) is an isomorphism
(M,S)→(M,S). It is strong,
if g is the identity.
- The space (M,S) is called homomorphic /
isomorphic to the space (M',S') if there is a
homomorphism / isomorphism.
Implications:
- (M,S) is isomorphic to (M',S') ⇔ (M',S') is isomorphic to (M,S)
So we may say: (M,S) and (M',S') are isomorph.
- If (M,S) is homomorphic to (M',S') and vice versa, then they are isomorphic.
(The author could prove this only with the axiom of choice.)
Symmetries of parts (part-symmetries)
Definition
- For a symmetry space (M,S) and a set M'⊆M (the part) the
set of symmetries of M' is
S'=sym(M,S,M'):={s∩(M'×M')|s∊S ∧ s^(M')=M' ∧ s-1^(M')=M'}
(For s^ see Notations.)
Implications
- (M',S') is a symmetry space
- If M'=M then S'=S.
Fixpoints
A fixpoint x of (M,S) fullfills ∀s∊Ss(x)=x.
Orbits
Definition
- For x∊M and s∊S the s-orbit of x (orbit(x,s))
is the smallest set o with x∊o and s^(o)=o and s-1^(o)=o.
- For x∊M the S-orbit of x (orbit(x,S))
is the smallest set o with x∊o ∧
∀ss∊S (s^(o)=o ∧ s-1^(o)=o).
Corunners
Definition
- ∀x,y∊M (x and y are corunners) :⇔
(∀s∊S (s(x)=x ⇔ s(y)=y))
- The set of corunners of x in the same S-orbit is called
bunch(x).
Subspaces
This chapter is experimental and not used elsewhere in this article.
Definition
- A subspace or
symmetry subspace (sss) of (M,S)
is a pair (M',S') with a set M'⊆M,
its symmetries S'=sym(M,S,M') and the conditions
- ∀x∊M', s∊S (s(x)∊M' ⇒ s∩(M'×M')∊S')
- ∀x∊M ∃s∊S x∊s^(M')
- The subspace (M',S') of (M,S) is proper
if it is not isomorphic to (M,S).
,
,
,
Comments
- The definition is intended to give similar subspaces as the usual
special definition, but there are discrepancies.
So we sometimes destinct "symmetry subspaces" und "usual subspaces".
Maybe a better definition of symmetric subspace can be found.
- Each symmetry space (M,S) is a subspace of itself.
- The empty symmetry space (∅,{∅}} is no subspace of
other symmetry spaces.
Examples
- Linear spaces
- y
- Affine spaces
- y
Geometric spaces
The examples have small dimensiosn, but can be extended to higher dimensions.
We use the following projections between a unit sphere and a plane:
- Orthogonal to a plane through the equator or tangent to a pole
- Central from the north pole to a plane through the equator or tangent
to he south pole. The plane is closed by an infinite point.
- Central from an equator point to a plane through the axis or tangent
to the opposite. The plane is closed by an infinite point.
- Central from the sphere center to a plane tangent to the south pole.
The plane is closed by an infinite circle where
opposite points are identified.
The following spaces are all symmetry spaces and are used for
realizations of polytopes.
Sphere,
elliptic plane,
conformal plane,
euklidean plane,
hyperbolic plane,
extended hyperbolic plane,
extended hyperbolic 3-space
Sphere
Elliptic plane
Conformal plane
Euklidean plane
The space may be realized as an affine space of dimension 2.
The projection 2 transformes the circles of the plane to circles
of the sphere and the circles of the plane to circles of the sphere
that cross the north pole. The reflection at lines in the sphere
are transformed to reflections at these spheres.
Hyperbolic plane
Extended hyperbolic plane
Extended hyperbolic 3-space
Literature
| [1] | Peter McMullen, Egon Schulte: Abstract regular polytopes. Cambridge university press (2002) |
| [2] | Branko Grünbaum: Regular polyhedra - old and new. Aequationes Math. 16(1977), 1-20 |
| [3] | Xiliang Bao, Francis Bonahon: Hyperideal polyhedra in hyperbolic 3-space. Bull. Soc. math. France 130 (3), 2002, p. 457-491 |
| [4] | H.S.M.Coxeter: The beauty of geometry. Dover publications inc, Minesota, New York, 1968 |
| [5] | Article 10 of [4]: Regular honeycoms in hyperbolic space. Reprint of: Proceedings of the international congress of mathematiciants, Amsterdam, 1954 (Vol. III) |
| [6] | Yunhi Cho and Hyuk Kim: The analytic continuation of hyperbolic space.
http://arxiv.org/abs/math/0612372v1, 2006 |
| [7] | Conformal geometry. G.V. Bushmanova (originator), Encyclopedia of Mathematics. URL: http://www.encyclopediaofmath.org/index.php?title=Conformal_geometry&oldid=16231 |