Polytope - Einstieg in die Theorie für alle Leser

Kira S   Willkommen   Bilder   Modelle   Theorie   Forum  

Einstieg   Vertiefung   Notation   Erkenntnistheorie   Mathematik  

Inhalt

• Übliche regelmäßige Polytope
• Graphen zu den Polytopen
• Polytope mit Überschneidungen
• Gebogene Polytope
• Fast regelmäßige Polytope

Übliche regelmäßige Polytope

Als Oberbegriff dieser zwei- bzw. dreidimensionalen Objekte gibt es das Wort "Polytop" (viele ...?) für Objekte beliebiger Dimension. So ist die Linie eindimensional und der Punkt nulldimensional. Aus formalen Gründen ergänzen die Mathematiker noch das -1-dimensionale leere Polytop L. Die letzteren haben zwar nicht viele Teile, trotzdem wird das Wort "Polytop" benutzt.

Unsere Erfahrungswelt ist zwar nur dreidimensional, aber Mathematiker haben keine Probleme mit 4- und mehrdimensionalen Polytopen. Darauf wird bei der Vertiefung eingegangen.

Polytope kleiner Dimension

Das leere Polytop L  mit der Dimension -1  Ein Punkt mit der  Dimension 0 Eine Strecke (Dimension 1) mit  zwei Endpunkten (Dimension 0)

Regelmäßige n-Ecke (Polygone; Polytope der Dimension 2)

gleichseitiges Dreieck {3} 3 Ecken und 3 Kanten Quadrat {4} 4 Ecken und 4 Kanten regelmäßiges Fünfeck {5} 5 Ecken und 5 Kanten regelmäßiges Sechseck {6} 6 Ecken und 6 Kanten regelmäßiges Siebeneck {7} 7 Ecken und 7 Kanten

Platonische Körper (regelmäßige Polyeder; Polytope der Dimension 3)

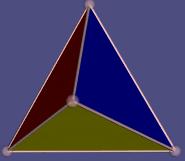
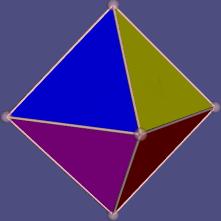
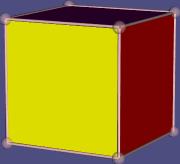
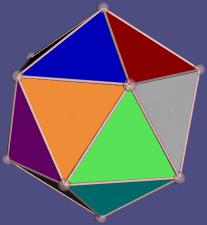
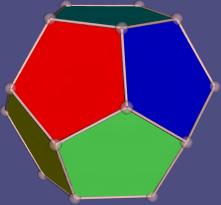
Tetraeder {3,3}, dreiseitige Pyramide mit 4 Ecken, 6 Kanten und 4 Dreiecken Oktaeder {3,4}, Doppelpyramide mit 6 Ecken, 12 Kante und 8 Dreiecken Hexaeder {4,3}, Würfel mit 8 Ecken, 12 Kanten und 6 Quadraten Ikosaeder {3,5} mit 12 Ecken, 30 Kante und 20 Dreiecken Dodekaeder {3,5} mit 20 Ecken, 30 Kanten und 12 Fünfecken

Die geschweiften Klammern mit den Zahlen darin hat der Schweizer Mathematiker Schläfli um 1850 für zwei- und mehrdimensionale Polytope eingeführt ("Schläfli-Symbol"). Bei einem normalen Polygon wird nur die Zahl der Ecken in die Klammer gesetzt. Bei den Platonischen Körpern steht vor dem Komma die Zahl der Ecken jeder Fläche und dahinter die Zahl der Kanten, die sich an einer Ecke treffen.

Die "Umgebung einer Ecke" im Polyeder besteht aus den Nachbarecken und dazu Verbindungskanten für Nachbarpaare, die auf derselben Fläche liegen. Beispiel: Beim obigen Würfel ist die vordere Ecke mit drei anderen verbunden. Diese bilden ein Dreieck, dessen Seiten Diagonalen der drei sichtbaren Quadrate sind. Im Schäfli-Symbol {4,3} bezieht sich der vordere Teil auf die Quadrate des Würfels und der hintere Teil auf die dreieckige Eckenumgebung.

Graphen zu den Polytopen

Hier und bei den Modellen gibt es zu den Polytopen drei Sorten von Graphen: Ecken-Kanten-Graph, Face-Graph und Flag-Graph.

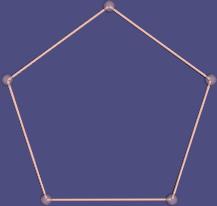
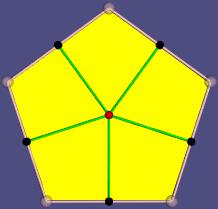
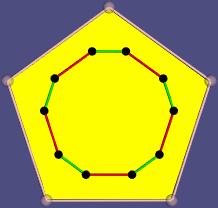
Fünfeck / Würfel	Ecken-Kanten-Graph	Face-Graph mit Vierecken	Flag-Graph im Polytop

1. Ecken-Kanten-Graph: Er hat als Knoten die Ecken des Polytops und als Kanten dessen Kanten. Beide werden hier weiß dargestellt.
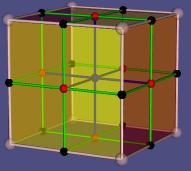
2. Face-Graph: Die Knoten des Graphen sind alle Teile (Ecken, Kanten, Flächen) des Polytops und das Polytop selbst. Sie werden im Englischen faces genannt. (Zur Veranschaulichung der Knoten werden weiße, schwarze, rote und blaue Kugeln benutzt, die bei den Ecken bzw. Mittelpunkten sind.) Jeder Knoten wird mit seinen direkten Teilen verbunden: ein Körper mit seinen Flächen (blaue Linien), die Fläche mit ihren Kanten (grüne Linien) und die Kanten mit ihren beiden Ecken (weiße Linien).

   Die Bildern zeigen, dass jede Polytopfläche in Vierecke zerlegt wird. Jedes hat als Ecken eine Ecke der Fläche (weiß), die Mittelpunkte der anliegenden Kanten (schwarz) und den Flächenmittelpunkt (rot). In den Körpern gibt es weitere Vierecke, gebildet von einem Kantenmittelpunkt (schwarz), den Mittelpunkten der beiden anliegenden Flächen (rot) und dem Körpermittelpunkt (blau, Farbe hier durch die davor liegende Fläche verfälscht).

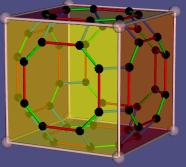
3. Flag-Graph: Seine Knoten sind die Flags. Ein Flag (nach dem englischen Wort für Flagge) ist hier eine Zusammenfassung von einer Ecke, einer anliegenden Kante und einer daran anliegenden Fläche. Es wird dargestellt als Mittelpunkt des Dreiecks, das die Ecke, den Kantenmittelpunkt und den Flächenmittelpunkt als Ecken hat.

   Diese Dreiecke sieht man, wenn man beim Face-Graph die Vierecke durch Diagonalen in Dreiecke teilt (also rote und weiße Punkte verbindet). Beispiel: Die enlische Flagge ist vereinfacht ein Rechteck mit einem Kreuz und Diagonalen darin. Dazwischen sind die hier gemeinten acht Dreiecke.

   Zwei Knoten werden miteinander verbunden, wenn sie sich nur in einem Teil unterscheiden.

   Die entsprechenden Dreiecke sind dann benachbart. In der Darstellung werden drei verschiedene Farben benutzt:

   • rot: Fläche und Kante gleich, verschiedene Ecken
   • grün: Fläche und Ecke gleich, verschiedene Kanten
   • blau (nur bei Körpern): Ecke und Kante gleich, verschiedene Flächen

   Der Flaggraph zu einem Polygon hat doppelt so viele Ecken wie dieses (z.B. 8 bei der englischen Flagge). Bei den Polyederen sind sie als rot-grüne geschlossene Linien auf den Flächen zu sehen. Zusätzlich gibt es um jede Ecke eine grün-blaue geschlossene Linie, die auf jeder Fläche zwei Punkte hat, und bei jeder Kante ein rot-blaues Viereck.

Polytope mit Überschneidungen

Unten sind regelmäßige nicht konvexe Polytope abgebildet. Das einfachste ist das Pentagramm. Es hat fünf Ecken und fünf sich gegenseitig schneidende Kanten. Es ist nach obiger Definition nicht konvex, da die Verbindungen zweier nah beieinander liegenden Ecken außerhalb des Pentagramms verlaufen. Die Faces sind durch die Fläche nicht eindeutig bestimmt, da dieselbe Fläche auch ein Zehneck sein kann, dessen Rand aus zehn Kanten besteht. Die Färbung im Bild veranschaulicht aber, dass das innere Fünfeck zweimal umlaufen wird.

Die Schläfli-Symbole {5/2}, {7/2}, {7/3}, {8/3} usw. haben außer der Eckenzahl einen "Nenner". Er gibt an, wie viele Ecken weit eine Kante reicht.

Für das normale Fünfeck könnte man auch {5/1} oder {5/4} schreiben, für das Pentagramm auch {5/3}, das ist aber beides nicht üblich. Als Nenner kommen deshalb nur Zahlen vor, die größer als 1, kleiner als die Hälfte der Eckenzahl und teilerfremd zur Eckenzahl sind. Wenn sie einen gemeinsamen Teiler>1 haben, wird die Ausgangsecke zu früh wieder erreicht. Z.B. {6/2} und {8/2} wären doppelt umlaufene Drei- und Vierecke. Die werden hier nicht betrachtet.

Regelmäßige nicht konvexe Polygone

Pentagramm {5/2} 5 Ecken und 5 Kanten {7/2} 7 Ecken und 7 Kanten {7/3} 7 Ecken und 7 Kanten {8/3} 8 Ecken und 8 Kanten

Regelmäßige nicht konvexe Polyeder, entdeckt von Kepler und Poinsot, jeweils mit allen, sich gegenseitig schneidenden Flächen und mit nur einer der Flächen.

{3,5/2}, 12 Ikosaeder-Ecken, 30 Kanten und 20 Dreiecke {5/2,5}, 12 Ikosaeder-Ecken, 30 Kanten und 12 Pentagrammecke {5/2,5}, 12 Ikosaeder-Ecken, 30 Ikosaeder-Kanten und 12 Fünfecke {5/2,3}, 20 Dodekaeder-Ecken, 30 Kanten und 12 Pentagramme

Gebogene Polytope

Fast regelmäßige Polytope